Wave Motion

Introduction

I propose to show in this Memoir, that there is an infinity of curves other than the collection of elongated cycloids, which satisfy the problem in question. I always suppose first, that the movements or vibrations of the string are very small... Second, that the string is uniformly thick along its whole length. Third, that the tension force F is a constant ratio to the weight of the string...the general equation of the curve is therefore

y = Ψ(t + s) + Γ (t-s)

— D'Alembert, Research on the curve formed by a taut string set in vibration, 1746

Wave Properties

We continue our investigation of periodic motions, looking now at waves and their properties. For the moment and for chapter 12, Sound, we consider mechanical wave motion. However, the same principles apply to wave motions in the propagation of light.

Waves

We describe waves in terms of their amplitude, wavelength, frequency, and velocity. The diagrams below show how amplitude and wavelength are measured.

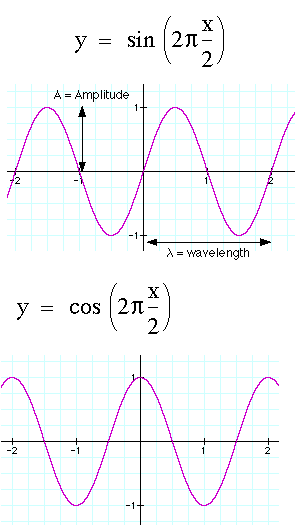
Here I have plotted the sinusoidal wave y as a function of x, measured in radians. In most physics situations, we will be plotting displacement from some zero point (y) as a function of time (using x as the time axis). The amplitude of the wave is its height, the length of the wave is the distance between two successive similar points (in this case, rising nodes). The argument for the sin or cos function is related to frequency (recall that we had the general case displacement x = A sin ωt + δ = A sin 2π* f * t, where f is frequency and t is time. In the graphs above, I have incorporated 2π into the argument, so nx = f * t.

Compare the amplitude at x = 0 (or t = 0) for the cos function and the sin function. By choosing the appropriate function we can map the initial conditions onto an appropriate sinusoidal wave, as we discussed in the previous lecture.

Notice what happens as I play with the values for amplitude and frequency.

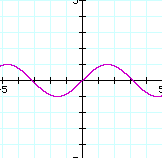
	y = sin x where x is in radians, so that one wavelength is 2*π ~ 6.28. The distance between nodes in this case is lambda/2 = π, or 3.14159...
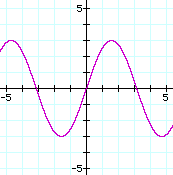
	y = 3 sin x; note the change in the height of the wave. For the general equation y = A sin x, A is amplitude.
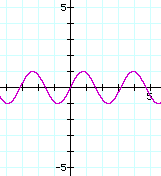
	y = sin 2x; note the change in frequency and wavelength. By increasing the argument to the sin function, I have increased the number of waves per x distance and decreased the wavelength by half.

A wave of form 1/2 sin x/2 will have what amplitude and wavelength compared to a wave of form sin x?

Wave Velocity

The velocity of a wave is a function of wavelength and frequency: v = λν, where the Greek letter ν (nu) is used for frequency. The speed of a wave in a given medium is constant for the medium in a particular state. Changes in temperature and density may affect the speed of the wave, but if these factors are held constant, than the speed will be constant, and any change in frequency will be compensated by a change in wavelength.

String	The velocity of a wave on a string is a function of the tension on the string and the density of material in the string, measured in terms of mass per unit length	v = sqrt (Tension / (mass/length)) v = sqrt (T/(m/L))
Solids	For bulk solids, the velocity of the wave is not surprisingly a function of the elasticity of the solid, that is, the compressibility of the solid in the direction of wave propagation, and its density.	v = sqrt (E /ρ)
Gases and Liquids	For gases and liquids, the velocity of the wave is a function of the compressibility of the medium, and so is related to the bulk modulus (compressibility in all directions) and the density of the medium.	v = sqrt (β/ρ)

Types of waves

There are two major types of waves:

Transverse waves, in which the amplitude of the wave is expressed perpendicular to the direction of propagation of the wave. A vibrating string is an example of a transverse wave.
Longitudinal waves, in which the amplitude of the wave is expressed in the direction of the propagation of the wave. These are also called compression waves; sound is the primary example of a longitudinal wave.

Waves Carry Energy

All waves transmit energy. The amount of energy is directly related to the period of the wave—and hence to the frequency and wavelength of the wave. The intensity of the wave is a measure of the power (energy per unit of time) transmitted across a given surface area, so Intensity = Power/Area. For waves which propagate in two or more dimensions, I = power/4*π*distance²—that is, it decreases as the distance from the source increases and the wave energy is spread out over more and more surface area. For waves which propagate in one direction (along a string, for example) the energy is not dissipated over increasingly greater area, and so the amplitude of the wave does not decrease unless it is damped by other forces.

We can relate the amount of energy in a spring oscillation to frequency by recognizing the relationship between period and k for a spring, and between energy and maximum amplitude A.

\begin{array}{l} T = 2 π \sqrt{\frac{m}{k}} \\ T^{2} = \frac{4 π^{2} m}{k} \\ k = \frac{4 π^{2} m}{T^{2}} \\ E = k \frac{A^{2}}{2} = \frac{4 π^{2} m}{T^{2}} \frac{A^{2}}{2} = \frac{2 π^{2} m A^{2}}{T^{2}} \end{array}

Energy is a function of both period and amplitude.

Reflection and Refraction

Constrained waves traveling in on dimension reflect off a surface in two ways. If the point at which the wave strikes the surface constrains the wave, the reflection will be phase shifted 180º. If there is no constraint, the wave is reflected without a phase shift.

Consider a string fastened to a ring which is anchored to a pole and unable to move. An incoming "up" pulse will reflect backwards as a "down" pulse.
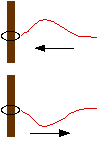
If the string is free to move, however, the wave is reflected without a shift.
Unconstrained waves of 2 dimensions will reflect off plane surfaces without a phase shift, but will change direction. The law of reflection, which was known to the ancient Greeks, states that the angle of reflection is equal to the angle of incidence in such cases.

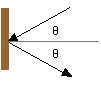
Refraction occurs when a wave passes through an interface between two media of different densities. The wave changes speed, which in turn cause it to bend. Diffraction occurs when a wave passes around the edges of a barrier. The edges act as new point sources of the wave, and the resulting new waves may interfere with one another in interesting ways. We'll investigate these situations in more detail when we discuss light waves and the optics of lenses.

Superposition

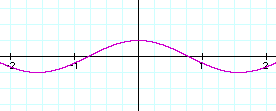
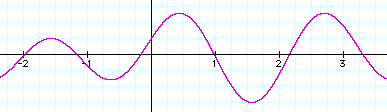
The table below shows the affects of superimposing two sinusoidal waves. According to the Fourier theorem, any sinusoidal wave, no matter how complex, can be represented by a sum of sin and cos functions with the appropriate amplitude and frequency values. This makes it possible to break down and analyze complex signals—sound waves, light waves, and other kinds of mixed wave motion.

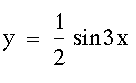
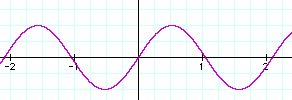
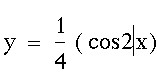
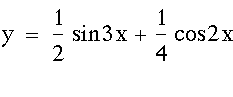
Amplitude or distance above the x axis is positive; amplitude below the x axis is negative. The sin function yields y = 0 at x = 0, but the cos function has a value of 1 at x = 0, so the sum of the amplitudes at x = 0 is 1. At x = -1.5, the sin function is nearly 2, but the cos function is -1, so the resulting wave has a amplitude of 1 at that point. On the positive side of the y-axis, the antinodes (high points) are reinforced. The amplitude of the superimposed waves at 0.5 is about 0.6, the sum of the 0.5 value of the sin function and the 0.1 value of the cos function. Where the amplitude is increased, the wave is in phase and constructive interference occurs. Where the amplitude is decreased, the waves are out of phase and destructive interference occurs.

Practice with the Concepts

Discussion Points

Is the acceleration of a simple harmonic oscillator ever zero? If so, where?
Real springs have mass. Will the true. Infrequency be larger or smaller than given by the equations for a mass oscillating on the end of an idealized massless spring?

© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.

Physics

Chapter 11: 7-11