
Physics
Chapter 8: 7-9

Web Lecture
Rotational Kinetic Energy and Angular Momentum
Introduction
At the time when Leonhard Euler was working out the implications of Newtonian mechanics for rigid bodies, there was not yet a widely accepted mathematical definition for energy, particularly kinetic energy. Newton understood that momentum p = mv was conserved, and Leibniz understood that vis viva, or mv2 was conserved. Euler recognizes the relationship between Iα and vis viva as a measure of kinetic energy after determining the velocity and inertial moment of three-dimensional rigid body rotating around three axis (hence the angles below of θ, η, and δ).
On account of which this expression must return a minimum
(( P sin δ - Q cos δ) sin θ - R sin (δ + η) cos &theta)2
aa cos2 η cos2 &theta + bb sin2 η cos2θ + cc sin2θ
[naively, we may consider this expression as the square of the torque applied divided by the moment of inertia : torque = τ = Fr=Iα; hence τ2 = (Iα)2/I.
This last quantity is proportional to the vis viva or the kinetic energy, on taking the angular velocity arising proportional to the angular acceleration α , which is now minimised]
Leonhard Euler, Theoria Motus corporum Solidorum Sue Rigidorum Vol 1. Chapter 9
Outline
Angular Momentum
Moments of Inertia
Before we go blithely off to solve rotational dynamics problems, we need to take a closer look at the force component of our torque definition. We started this lecture with the realization that rotational motion occurs because force is exerted "off-center". While we stuck to translational motion, we could assume all the mass operated on by our linear-motion producing force was at the geometric center of mass of the object, and that the force operated on this center, as though we had a point mass; F = ma was all that we needed.
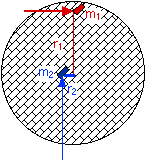
We can no longer make that assumption for rotational forces. Consider the merry-go-round at left. Mass m1 near the perimeter requires a larger torque force than m2 near the center, since its radius distance r1 > r2. This is reflected in our formular for torque: if we substitute the angular term for acceleration for the linear one and consider r as always at right angles to F, then
F X R = ma * r becomes
F =mr α * r .
The term I (for inertia) is used for the sum of all the little masses, each at its own distance r:
I = Σ (mr2).
Our torque formula becomes τ = I α.
The calculation of moments of inertia is properly the province of integral calculus, which allows us to sum up all the m x r components. For now, we will build on the work of those who have come before us; in figure 8-16 of the text are the moments of inertia for a number of common solid geometrical shapes. (Those of you who want a more extensive list will find one on the Wikipedia List of Moments of Inertia page. There is also an excellent summary in the Hyperphysics Textbook at the University of Georgia.)
A useful technique, which simplifies the process, is to determine the radius of gyration for different shapes. Let's assume we have an oddball shape. We calculate its moment of inertia I, then set this value equal to Mk2, where M is the total mass of the object. The astute reader who has gone to the trouble of looking at figure 8-16 will immediately recognize Mk2 as having the same form as moment of inertia for a hoop of radius k. We can thus create some useful equivalencies between interesting objects and the hoops which would have the same moment of inertia as each object. Then k is equivalent to the radius of our imaginary hoop; this distance k is the radius of gyration for our object.
Energy and Momentum
Finally, we consider energy and momentum in the case of angular motion and torques. As with linear situations, both rotational energy and angular momentum will be conserved, which greatly simplifies analysis of many situations. We substitute I (the moment of inertia) for the mass, and ω for the velocity in the linear equations to get the angular motion equivalents.
The kinetic energy for a moving, spinning body is the KE of its translational motion, mv2/2, plus the kinetic energy of its spinning motion, which is (not surprisingly) I ω2/2. Most of the difficulty in dealing with energy problems involving rotational motions lies in determining the moment of inertia, or converting the angular velocity to the proper format (radians per second), before doing the calculations.
Angular momentum L is I ω. Recall that for linear momentum, we also had the relationship ΔF = Δp / Δt. We can make a similar analogy for torque Δ= ΔL / Δt: that is, torque is a measure of the rate of change in angular momentum, and momentum remains constant if the torque is zero. This allows us to use conservation of angular momentum to analyze situations where the angular velocity is not changing, but the radial distribution of the mass is changing. Since
L = I ω = sum (m*r2), if r decreases while L remains constant, then ω must increase.
The classic example is the spinning ice skater, who pulls her arms in and up over her head (decreasing I significantly) in order to spin faster and faster, then puts her arms out to slow herself down.
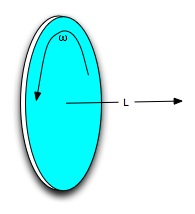
Conservation of angular momentum keeps you upright on your bicycle. Because L is a vector (pointing in the direction of the torque) and the laws of inertia say that objects in motion will resist changes to their state of motion, changing the direction of the torque meets with resistance just as changing the magnitude of the torque does. The bicycle wheel spins in the vertical plane, and L points out of this plane. "Falling over" would change the direction of L, so inertia will resist this change somewhat--usually enough for you to have time to shift your own weight and keep the bike upright. Notice that since L is direction proportional to ω, the faster you go, the less you are likely to fall sideways. The added "security" carries a proportional risk: when you do fall, all that Iω2/2 kinetic energy will go into disrupting the metallic bonds that hold the frame together in the bike and the chemical bonds that hold your tissues together when you hit the ground. [Knowing this is not very comforting when you do fall.]
Conservation Laws and Analytic Methods
You should by now have come to the conclusion that orthogonality is a very important tool in breaking down complex situations into parts that you can analyze separately. Two vectors are orthogonal if they are at right angles to one another. An extension of this principle means that in any situation involving both linear and rotational motion, we can analyze and apply conservation of energy and conservation of momentum to the linear components independently of the rotational components of motion. The two are related through the linear velocity v of a mass m at distance r from the center of motion: v = ω x r, so we can use that relationship to transfer what we know of v to rotational motion or what we know of ω back to translational motion for m.
Practice with the Concepts
Discussion Points
- A shortstop may leap into the air to catch a ball and strode quickly. As he throws the ball the upper part of his body rotates. If you look quickly you'll notice that his hips and legs rotate in the opposite direction. Why?
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.