Forces Resulting in Circular Motion

Introduction

Outline

• Circular Motion
  • Uniform Circular Motion
  • Using Angular Variables
  • Circular Dynamics
• Practice with the Concepts
• Discussion Points

We've looked at straight line motion, so now we take a look at things that look in perfect circles. In the real world, objects move in neither perfectly straight lines or perfect circles or with constant acceleration, because such motion requires a completely isolated system on which no outside forces are working. Nevertheless, our investigations into these simplified situations will help us understand the more complicated real ones.

Circular Motion

Since the beginning of the term, we have looked at acceleration along the vector direction or opposite to it (deceleration). Acceleration along the velocity vector affects only the magnitude of the velocity (speeding up and slowing down), not its direction. But changes in either velocity or direction are both considered acceleration.

Now we look at what happens when a force acts on a moving body at some angle to that body's motion. This chapter considers first changes in direction which do not affect the speed of an object--uniform circular motion. We can create situations where this occurs by spinning objects, like a ferris wheel, or a merry-go-round, or a centrifuge, at a constant rate. More significantly, such accelerations arise from the mutual attraction of masses on one another, such as the earth on the moon, or the sun on the planets. They also occur when charged particles move in an electrical or magnetic field, a subject we study in detail later in this course.

Gravity and electromagnetic forces are two of the four natural forces; classical physics deals with the resulting motions of objects affected by these forces, so long as the speeds are much below the speed of light. Relativity deals with these forces at speeds approaching that of light, and nuclear physics and quantum mechanics deal with the other two forces--the weak and strong nuclear force. One of Einstein's greatest efforts went into trying to understand if these forces are actually different manifestations of the same universal force which could be explained by a grand Unified Field Theory. While some current research in cosmology indicates the possibility of relationships between the nuclear forces, no one has yet been able to explain all four forces with a single theory.

Uniform Circular Motion

In the special case where a force acts with constant acceleration toward a fixed point on an object already in motion, the object moves in a circle around the point. In the absence of the acceleration, the object would continue in a straight line; it is the force which "bends" the velocity, giving the object an component toward the center while not affecting its tangential velocity.

Study the standard circular motion diagram below (similar to 5.2 in the text).

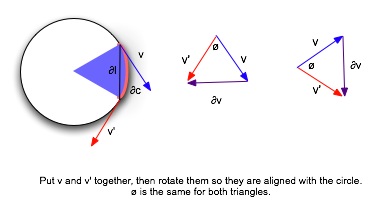
Since both triangles are isosceles triangles with equal angles, they are proportional. The actual distance traveled by a body on the circle is the arc (between the start of v and the start of v'); the approximation from the triangle is the chord δl. As we consider points closer and closer to each other on the circle, δv and δl both become very small; and δl approximates more closely the actual distance traveled. From similar triangles, δv/v ~ δl/r; at the limit where φ goes to zero, the two quantities are equal.

We can then rearrange δv/v = δl/r to δv = (v/r) * δl.

Acceleration is δv/δt, so if we substitute these values in, we have

a_R = δv/δt = (v/r) * δl/δt.

But, as we have already noticed, at the limit δl is the actual distance traveled along the arc, so δl/δt is actually just v.

a_R = (v/r) * δl/δt = (v/r) * v = v²/r

The ramifications of this relationship are rather interesting. Increasing the velocity means that we have to increase the acceleration (by increasing the force) in order to keep the object in a circle with a constant radius....or, if we can't increase the force, the circle with automatically increase in size.

Or, to put it another way, if we increase the size of the circle without changing the velocity, accleration will decrease--because the velocity vector is not changing direction as fast as it was when the circumference of the circle was tighter.

Notice that in uniform circular motion, the velocity and acceleration are always at right angles to one another. Acceleration has no component along the direction (either positive or negative) of the velocity vector, so the magnitude of the velocity does not change, only its direction.

The circumference of the circle is 2 * π *r. If the period to complete one revolution around the circle is time T, then the velocity (constant magnitude) is distance/time = 2*π*r/T.

Using Angular Variables

Obviously, φ and the distance along the chord are related. If we use radians (one radian is an arc whose length equals the radius r of the circle), then φ = l/r. This allows us to equate the angle to the length along a circle of radius r for that angle.

We can also express velocity in radians: δφ/δt = angular velocity (usually expressed with the Greek symbol omega ω). Angular acceleration is then the change in angular velocity per unit time: δω/δt = α = a_R.

Circular Dynamics

Assume that we want to keep a body moving with the same speed but in a circle of fixed radius. What force is necessary?

Well, we have accleration = v²/r, so if F = ma, then F_c = ma_c = m v²/r. We can now use this in our free-body diagrams to analyze situations involving circular motion, such as cars accelerating around a corner, or weights on a string (see the lab).

Practice with the Concepts

Discussion Points

• Earth is not quite an inertial frame. We often make measurements in a reference frame fixed on the Earth, assuming Earth is an inertial reference frame [Section 4–2]. But the Earth rotates, so this assumption is not quite valid. Show that this assumption is off by 3 parts in 1000 by calculating the acceleration of an object at Earth’s equator due to Earth’s daily rotation, and compare to g = 9.80 m/s², the acceleration due to gravity.

---

© 2005 - 2024 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.