
Physics
Chapter 2: 6-8

Homework and Lecture
The Mathematics of Kinematics
Graphing Solutions
Introduction
Omnis qualitas, si fueri uniformiter difformis, ipsa est tanta quanta foret qualitas eiusdem subiecti vel equalis uniformis secundum gradum puncti medii eiusdem subiecti; et hoc intellig si qualitas fuerit linearis. Et si fuerit superficialis, secundum gradum linee medie; si vero fuerit corporalis, secundum gradum medie superficiei, semper conformiter intelligendo. Istud ostenditur primo de lineari.
Every quality, if it is uniformly difform, is of the same quantity as would be the quality of the same or equal subject that is uniform according to the degree of the middle point of the same subject. I understand this to hold if the quality is linear. If it is a surface quality, [then its quantity is equal to that of a quality of the same subject which is uniform] according to the degree of the middle line; if corporeal, according to the degree of the middle surface, always understanding [these concepts] in a conformable way. This will be demonstrated first for a linear quality.
- Nicole Oresme, Tractatus de configurationibus qualitatum et motuum
Outline
Medieval philosophers struggled with language to explain different types of motion. Uniform motion had what we would call a constant speed, although direction could vary. Difform motion described objects with changing speed. But there was the odd middle case, where motion changed in a predictable manner—uniform difform motion, what we would now say was an object under constant acceleration. Nicole Oresme eventually formulated a "mean speed theorem", anticipating Galileo's work on falling bodies. He recognized that for objects with uniform difform motion, the mean speed was the initial speed plus the final speed, divided by two: vmean = ½(vinitial + vfinal). To see how he worked this out graphically, take a look at the description of Oresme's work at The History of Science Online.
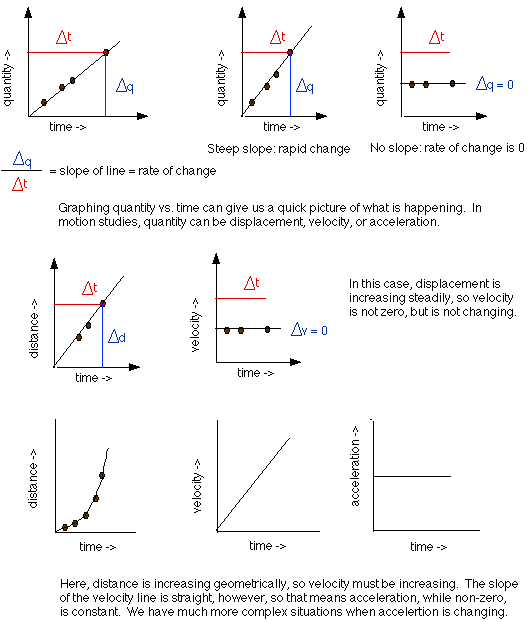
Learning to see a situation in different ways is very useful. The algebraic formulae equating displacement, velocity, and acceleration are one way to understand their relationships. Another way, as we have seen, involves graphing data and looking at the lines and the slopes of the lines that result from different situations. Practice evaluating graphs can help us quickly determine which way and how quickly a factor of motion is changing.
Graphing velocity and acceleration
A note on rates
We've actually accomplished quite a lot. The Greeks and medieval philosophers had a great deal of trouble trying to describe these changes in motion, and perhaps you can start to see why. The Greeks called displacement at at constant rate (velocity is not changing, accleration is zero) uniform motion. When velocity is changing, the motion becomes non-uniform, or difform motion. Now, acceleration can be a constant, with velocity changing at a constant rate: this is uniformly difform motion. Or acceleration can itself be changing, so that velocity changes at different rates: tis is difformly difform motion. Looking at the graphs below for rates may help you sort these situations out.
So far, we have talked about the rate of change of displacement as d/t = v, and the rate of change of velocity as v/t = a. But rates are used throughout science for any change in a quantity with respect to the amount of time it takes to make the change. Any time you see a reference to rate, you can plot the quantity with respect to time and notice some things about it:
Falling Bodies
Aristotle posed the problem this way: all matter has a special nature which pulls it toward or pushes it away from the center of the earth. Fire thus moves upward because it possesses a nature of levity; earth moves downward because it possesses gravity. Air has some levity, but not as much as fire, so it moves away from the center of the earth more slowly than fire. Water has less gravity than earth, so while it moves toward the center of the earth, earth itself will sink down throw water.
Assigning two different natures to different kinds of matter kept Aristotle and the philosophers who followed him from generalizing motion over all types of matter. That was the peculiar task of Galileo, who proposed a description of motion in which matter possessed only gravity, no levity, and in which all matter moved uniformly toward the center of the earth with a constant acceleration. He laid the foundation for modern mechanics with this realization, and determined empirically (without being able to show the cause), that the distance a body falls in a given time t is s = ½at2, where a is gravitational acceleration. In a series of experiments around 1600, Galileo determined that this acceleration was about 9.8 meters/second2 (although he used different units because the metric system hadn't been invented yet). Galileo and his contemporaries had a very practical use for this information. They needed to predict the projectile motion of balls thrown at rival Italian city-states by the newly invented cannons, so it was very important to understand exactly what would happen if the canon were pointed so high and the city wall was so many feet distant.
In such projectile motion, we have to determine what coordinate system or frame of reference we will use. The ball moves up (with gravity decelerating it) and then down (with gravity accelerating it). It doesn't matter whether we choose up or down as the "positive" direction, as long as we apply the direction consistently to both the velocity and acceleration vectors involved.

[Blue: displacement. Green: velocity. Gold: acceleration]
Consider a ball thrown in the air. In the upward half of the journey, the direction of displacement and velocity are both up, and acceleration is down. In the downward half of the journey, all three vectors are directed down.
However, notice that the magnitude of displacement increases; it is greates at the top of the path. The magnitude of velocity is decreasing during the first half, reaching zero at the top (the ball appears motionless at the top of its arc). The magnitude of velocity then increases as the ball comes down.
During the entire event, acceleration changes in neither magnitude or direction, since it is due to an unchanging force — gravity.
Problem Solving
Be sure to study the methods of problem solving outlined in the text. Use all the methods to help you understand the problem if you are having trouble.
Practice with the Concepts
Discussion Points
- Is the acceleration due to gravity really constant near the surface of the Earth? Why do we assume that it is for the problems in this chapter?
- In the flight of a projectile like a home run baseball, are horizontal and vertical components of velocity the same at each instant? If not, when is either a) at a maximum or b) zero?
- On a graph of velocity vs. time, why is the area under the velocity curve equal to the distance traveled?
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.