Chemistry
Chemistry 17: 1-3

WebLecture
The Common Ion Effect
Outline
- The Common Ion Effect and Buffers
- Titrations
- Practice with Concepts
- Discussion Questions
- Optional Website Reading
The Common Ion Effect and Buffers
We know that for solids dissociating into ions, where we can ignore the concentration of the solid reactant, we need only consider the concentrations of the products and their stoichiometric coefficients in calculating the solubility product Ksp:
CcDd → cC + dD
where C and D have the appropriate ionic charges for the species.
Consider now a solution that has a weakly dissociating salt, such as lead chloride.
PbCl2(s) ⇔ Pb+(aq) + 2Cl-(aq)
At equilibrium, the concentration of product ions gives a Ksp of 1.6 * 10-5, a very small number, indicating that the concentrations are small: lead chloride only weakly dissociates.
So for our lead chloride dissociation, we have
Now suppose that we add to this solution some sodium chloride. Sodium chloride dissociates completely at liquid water temperatures:
NaCl(s) → Na+(aq) + Cl- (aq)
Le Chatelier's principle says that the addition of a product to a reaction in an equilibrium state will cause the reaction to run backwards to reduce the product amount and restore the ratio of reactants to products that held at equilibrium. The solubility of the lead chloride decreases when the common product ion is present in the solution. This reduction in solubility of a weakly-soluble product is called the common ion effect.
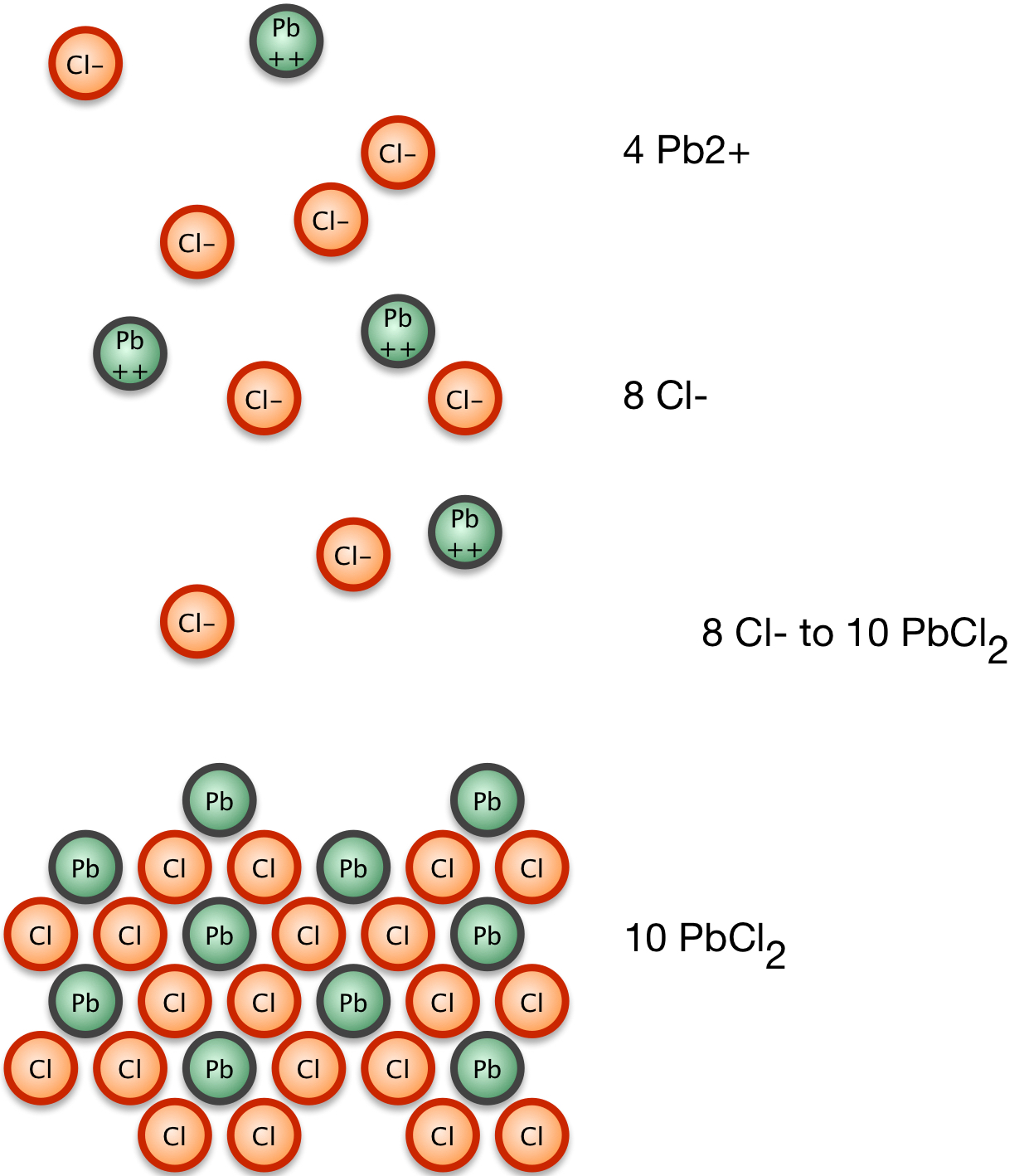
1. Lead chloride comes to equilibrium with Pb2+ and Cl1- ions
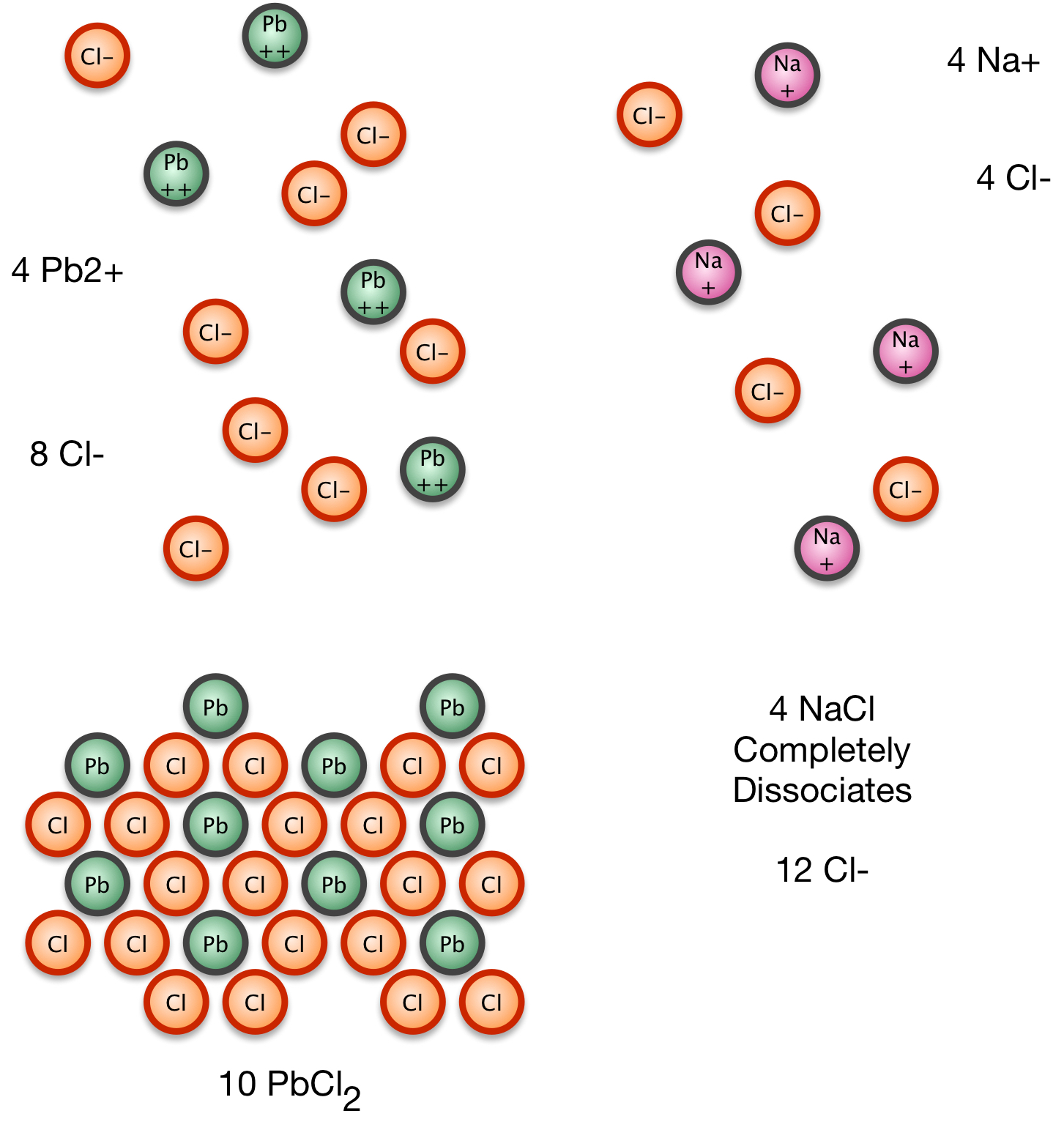
2. We add NaCl, which completely dissociates.

3. Some of the Pb2+ and Cl1- precipitate to move toward equilibrium; however, there's a balance to strike between loss of Pb2+ which are still in equilibrium above the solid and loss of Cl1- being driven to precipitation by excess Cl1-.
If we apply these principles to acid-base reactions, we have a similar result. Consider the reaction of carbon dioxide and water, which can dissociate to form a weak acid, carbonic acid, which can further dissociate to the bicarbonate ion (its conjugate base) and a hydrogen ion. Adding acid and excess H+ to the system will cause formation of carbonic acid; adding CO2 to the system will increase carbonic acid and the bicarbonate ion.
CO2 + H2O ⇔ H2CO3 ⇔ HCO-3 + H+
This relationship explains how blood maintains a constant pH. If the acid level of the blood rises, the body stimulates exhalation. Gaseous CO2 is pulled from the system through the lungs, and all the reactions run to the left, reducing the excess acid in the blood stream to normal levels. If the blood pH drops (becoming more basic), the kidneys excrete H+, forcing the reaction to run to the right in the remaining blood, conserving CO2 and raising the acidity to normal levels.
In this reaction, the HCO-3 ion is the conjugate base of the carbonic acid H2CO3.
Buffers
Consider the weak acid reaction AH which dissociates weakly to form a solution with all of the species present:
AH → A- + H+
If we add hydroxide, a strong base, it will drive the AH to continue to dissociate: the reaction until all the available hydroxide ions have been consumed. The equilibrium K for this reaction is large, since both AH and OH- are consumed and ultimately present in very small amounts at equilibrium.
AH + OH- ⇒ A- + H2O (aq)
If instead of hydroxide, we add the strong acid hydronium to the weak acid solution, it will react with the conjugate base A- present in solution. The equilibrium constant K for this reaction will also be large, since all the available H3O+ will dissociate.
A- + H3O+ ⇒ AH + H2O
So adding either a strong base or a strong acid to solution with a weak acid in equilibrium with its conjugate base ion will drive the reaction to reduce the added component significantly. Such a solution is a buffer; it will react to additions in such a way that it maintains its equilibrium as long as either acid molecules on conjugate base ions remain to react.
When an acid dissociates in water to form hydronium, we can write the equilibrium constant Ka:
We can solve this for the concentration of the hydronium ion:
But now, since we have [H3O+], we can solve for pH = -log[H3O+] by taking the logs of each side and negating them:
Since -log[H3O+] = pH, and -log (Ka) = pKa, we can rewrite this equation in a simpler form:
If we can assume that the concentrations of the acid and conjugate base do not change much from their initial concentrations, which will be true when the pH range is not too extreme (between 3 and 11) and the initial concentrations are so large that adding a small amount of acid or base will not shift the concentration much, then the above equation (known as the Henderson-Hasselbalch Equation) gives us the pH of the buffer solution.
Titrations
Titrations are a method of determining the acidity of a solution by adding small amounts of a concentrated known solution to a specific volume of the unknown solution. The two solutions react, and when all of the reactant in the unknown solution has been consumed, we've reached the equivalence point.
In a strong acid-strong base reaction, all of the acid dissociates and all of the base reacts, so there is the same amount of hydronium and hydroxide ions at the equivalence point: the pH of this reaction is 7.
When a weak acid reacts with a strong base, we have both the weak acid, its conjugate base, and the strong base present. The strong base reacts with all of the weak acid at the equivalence point, but the weak conjugate base ion is still present, so at the equivalence point pH > 7: the solution is basic.
When a strong acid reacts with a weak base, a similar situation occurs. The weak base is present along with its conjugate acid. All of the strong acid reacts with all of the weak base, but the conjugate acid remains, so at the equivalence point pH <7: the solution is acidic.
In either situation, halfway to the equivalence point the acid component and its conjugate base component are present in equal concentrations. The Henderson-Hasselbalch equation simplifies, because [acid]/[conjugate base] = (x)/(x) = 1, and log 1 = 0:
Obviously, it is important to know what the pH of a solution is at a given point, so that we can tell whether or not we have reached equivalency. We use indicators whose acid form is one color and whose conjugate base form is a significantly different color. When the indicator's acid concentration equals its conjugate base concentration, its pH = pKaind. If the concentration of the indicator acid form is greater than the conjugate base, the indicator will have its acid color. At the point where the indicator changes color, the base becomes more concentrated and the base color shows. So at the point at which the indicator color flips, the pH of the solution is equal to the pKaind — presumably something we know.
Purple or red cabbage contains a pigment called anthocyanin which changes color depending on the acidity of its solution. The neutral color is the normal purple of the cabbage leaf. The picture below shows what happens when acids (lead nitrate, copper sulfate, sulfuric acid, oxalic acid, apple cider vinegar, cream of tartar), and bases (ammonium alum, baking soda, ammonia, sodium hydroxide) of different pH values are added to the indicator. Paper strips used for pH detection are used to confirm the pH values.

Practice with the Concepts
Discussion Questions
- What is a buffer? Why is it useful?
- How does a titration help determine the concentration of a solution?
Optional Readings
Practice titrations with
- the Titration Simulator at Wake Forest University.
- or with this one McGraw Hill simulator.
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.