Chemistry
The Bohr Atom and Electron Quantum Mechanics

WebLecture
The Bohr Atom and Electron Quantum Mechanics
Outline
Atomic Structure
In the early twentieth century, Bohr introduced a simple model for the hydrogen atom, sometimes called the "planetary atomic model" because its electrons orbiting the nucleus in planar orbits resembles solar system planets orbiting the sun. While this model is not accurate (electrons orbit the nucleus using the full volume in complex interactions with each other), the model is still useful in helping us understand the limitations on electron locations within the atom, and the exchange of energy required to change orbitals.
The Bohr Atom
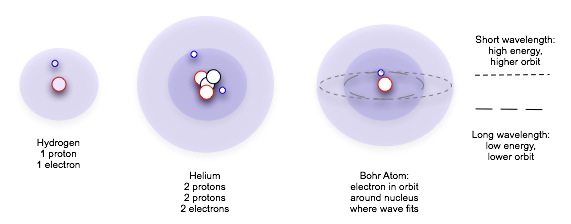
Work by Ernst Rutherford showed in the early decades of the twentieth century that the atom was mostly space, a cloud of negatively charged particles moving around a very small, positively-charged nucleus. Planck's theories of quantum mechanics suggested to the Danish physicist Niels Bohr that these electrons could not swarm just any way around the nucleus: they had to be in discrete —h that is, separate and identifiable — orbits. [Don't think of orbits as planetary orbits, mostly circles in a single plane; these orbits actually have bizarre shapes and are volumes in three-dimensional space.] A given electron could absorb only certain amounts of energy and change from one acceptable level to another, but not to any position in between.
Bohr was able to determine that the energy states of the electron were proportional, related to one another in whole-integer values. For the first energy (lowest energy) state of hydrogen, this value was -Rhc, where R is a constant equal to 1.097 * 10^7 per meter, and c is our friend the speed of light. The energy of the second level is 1/4 this, of the third level 1/9, so the amount of energy to jump between high level N and low level n (where both N and n are integers) is given by
The greater the difference between N and n, the larger E becomes. An electron moving from a higher level to a lower level gives off energy as light, the wavelength of light being determined by the Planck equation E = h c/l. An electron must absorb energy in exactly the right amount to move from a lower level to a higher one.
Spectra
We can think of an individual "beam" light as a wave traveling through space, much the way a wave of energy travels through water. The longer the wave, the less the energy it carries. With light, the wavelength translates to color: the longer the wavelength, the redder it is; the shorter the wavelength, the bluer it is. Actually, "light" is a general term for all electromagnetic radiation, which includes many wavelengths our eyes cannot see: from radio waves and the waves that heat your tea water in the microwave to the doctor's x-rays and gamma radiation from exploding galaxies now long gone. Each "beam" of light has a particular wavelength, and that wavelength is a specific amount of energy and a specific color.
| Now we look more closely at the Bohr atom, whose electrons are "circling" the nucleus at discrete distances. |  |
| Suppose we want to move an electron from an inner orbital to an outer one. We can't just pump any amount of energy in: the electron needs a specific amount to move outward to the next orbital. | 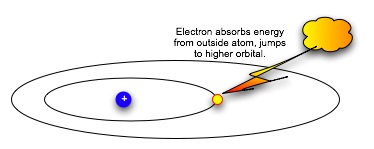 |
| Think of seats at the opera: the orchestra seats are $80 a performance, the third balcony rear are $12. The opera sales office will take checks for $80 or for $12, and put in you the right seat. But if you send them a check for $50, they do not make change: they return the check with a politely-worded letter asking you to remit the correct amount for the seat preferred. In the same way, the electron can absorb or emit a specific amount of energy that will let it jump to a particular energy level and orbital. Having absorbed the energy, when it emits the same amount of energy, it falls back to the original orbital. |
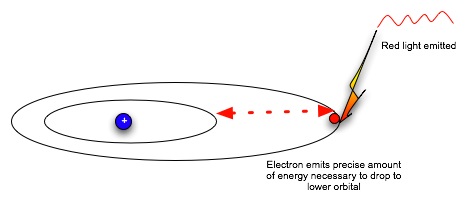 |
| Now the electron is in a lower, more stable orbit. It can not move to the higher energy level without absorbing energy again. Note that absorbing or emitting energy doesn't change the electron itself; it only changes the electron's energy level, which dictates how fast it moves and how far it can be from the nucleus. So an electron can absorb and emit energy over and over. |  |
| From light theory, we know that the amount of energy that an electron can absorb corresponds to a given wavelength, which in turn we interpret as a specific color. So we can think of the process this way: the electron absorbs a beam of green light, and jumps up and away from its home atom. In the case of the chemicals in the chloroplast (chlorophylls and carotenoids), the electrons absorb blue and red light. They don't respond to yellow and green light, so those colors are reflected by the cell, and the plant leaf made up of those cells looks green or greenish-yellow to us. | 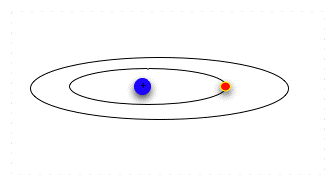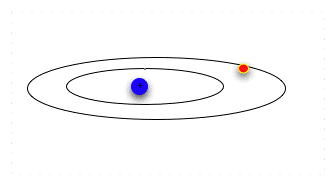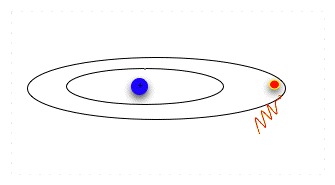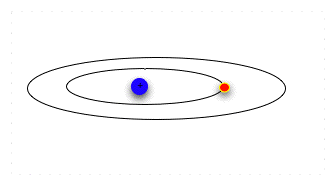 |
Each jump between orbits thus involves a specific amount of energy. For a bunch of atoms of the same element, the possible transitions are limited, so the possible wavelengths emitted or absorbed are also limited. A hot gas "glows" by giving only certain wavelengths off, and so has a characteristic emission spectra and a dominant color. You can easily see this by comparing color in the older bluish mercury street lights and the new yellow sulfur street lights.
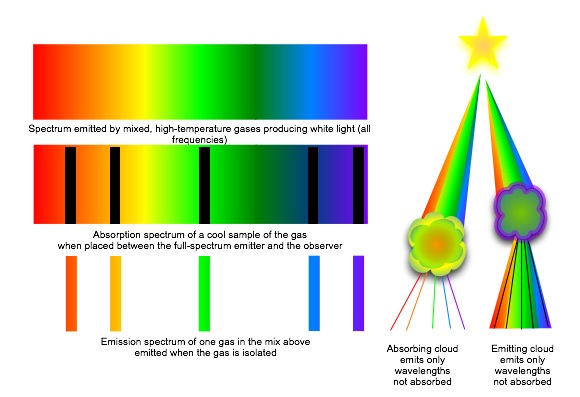
The spectra or set of colored lines given off by atoms or molecules of a hot substance is unique to the substance. Heating the substance (without changing its composition) does not change the distribution of spectral lines, but it does change their intensity (usually measured by their width). A very hot substance will have broader lines in the short wavelengths of its spectra, since more electrons will be in an excited state and able to drop from higher orbitals to lower ones. A cool substance will have narrow short-wavelength lines and broader long-wavelength lines, reflecting the fact that most of its electrons are jumping around the lower orbitals. By looking at the spectra then, we can identify not only what the substance is, but also what temperature it is.
So far, we've discussed emission spectra —the energy emitted by excited electrons falling to lower levels. But electrons can absorb energy as well. If we have a source which is so hot that the average temperature is capable of stripping electrons entirely from its molecules, the "free" electrons are not required to have specific amounts of energy. They can have any energy, and their collisions and energy exchanges result in a continuous spectrum. If we then put a cool gas near this source, the cool gas electrons will absorb energy, but only for those wavelengths which move the electrons properly between levels in the atom or molecules of the substance. Lines of color will disappear from the spectrum, as though someone had gone along drawing black lines with a magic marker. These absorption lines exactly match the position of the emission lines for the substance, so we can identify the absorbing gas just as we identified an emitting gas.
The Electron Wave
It was Louis deBroglie who finally put Planck's vision of the quantized photon and Bohr's vision of the discrete electron orbitals together with the realization of how the orbit of the electron was restricted to particular distances from the nucleus through the following derivation:
so
and
DeBroglie showed (using Einstein math for energy considerations, since we have particles traveling at relativistic speeds near c) that
h = mv * l [deBroglie equation]
(don't worry about the derivation now). This means that a particle with a particular momentum has an associated wavelength. Since h is a constant, the larger the mass, the smaller the wavelength; we can't detect it unless the mass is very small, on the order of an atomic sub-particle like an electron.
We now consider an electron at a given distance r from the nucleus of the atom. For simplicity, we will consider an electron in a mostly circular orbit (the analysis works for any shape orbit, but the math gets very difficult). From physics, we know that for the path of the charged particle in orbit around a charged nucleus to be stable,, the centripetal force Fc on the particle must balance the attractive electrical force Fe between the negative electron (charge q) and positive nucleus (charge Q):
In the centripetal force expression, me is the mass of the electron, v is its velocity, r is its distance from the nucleus.
In the Coulomb equation, k is a constant, q and Q are the charges of the electron and nucleus, respectively, and r is still the electron's distance from the nucleus.
What this equation tells us is that for the electron to be at a certain distance from the nucleus, it must have a particular velocity v. From the deBroglie equation, we can now get the wavelength associated with the electron: l = 2h/mv.
But if the electron behaves like a wave rather than a particle, the wave wraps around the nucleus along the circumference of the electron's orbit. When it gets all the way round, it acts like a physical wave, and the second lap interfers with or enforces the first lap. The wave will cancel itself into noise and nothing unless it fits the circumference exactly and reinforces itself. div class="box">To visualize this more easily, look at the Java applet on the deBroglie Mode at the Quantum Zone. This is one of my favorite websites and well worth exploring.
If we apply all of the concepts above to our electron, we will get a stable situation only where the path of the electron (in our current consideration, the circumference 2 * π * r of a circular orbit) is equal to some integer multiple of the wavelength:
But as we've already seen from deBroglie's equation, l = h/mv. So
Rearranging, we get
The momentum mv of the electron at a particular distance r from the nucleus is an integer multiple of a constant....which is what Bohr showed with the Rydberg equation.
Practice with the Concepts
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.