Chemistry
Chapter 5: 1-3

WebLecture
Thermal Energy
Outline
- Basic Energy Concepts for Chemistry
- Practice with Concepts
- Discussion Questions
- Optional Website Reading
Basic Energy Concepts for Chemistry
We've spent a lot of time talking about matter and how to measure it in various situations, but chemical reactions don't just involve rearrangement of matter. They also involve the transformation of energy from one form to another: heat energy from the environment into a reaction system to create higher-energy bonds between atoms in molecules, or heat, light, and sound energy released from chemical bonding energy as electrons shift to lower orbitals. Before we can discuss electron orbital transitions, we need to understand what energy is, how it behaves generally, and how it is related to chemical reactions. This gets us into the jungle of thermodynamics.
Note the language of the discussion of the laws of thermodynamics. Unlike the "law of gravity" that describes the attraction of matter for other matter, and which is assumed true for all matter in all parts of the universe, the laws of thermodynamics are statistical. They describe the probable behavior of a given system, that out of all possible states, a system is more likely to be found in certain types of states than others. They do not guarantee this behavior! The fact that a particular state has a low probability still means that it has a probability greater than zero, and could occur.
Of the many possible states for your room, there is one that passes your mom's inspection: everything in place, no trash, ready to be viewed by your Aunt Mildred or your grandmother. Since this is a possible state, it is theoretically possible that a passing tornado could leave your room ready for inspection. However, since there are many, many more disordered states possible, it is much more likely that any passing tornadoes will leave your room even more disorderly than it currently is. You will therefore probably have to do work [in chemical terms, spend energy] to get your room into an ordered state before the impending arrival of your relatives.
There are, of course, impossible states with zero probability that will never occur; we ignore these.
Energy runs downhill
One of the fundamental rules of the universe is that energy cannot be created or destroyed, a statement known as the law of the conservation of energy. Whatever amount of total energy there is in the whole universe is what we've got to work with: that amount is constant. Energy can, however, change form.
In all energy-conversion or transfer situations, the tendency is for the system to move to a state with lower energy, usually by transferring energy out of the system as heat, light, or sound, or by redistributing it so that individual components have less energy per component. You can think of this as the "water runs downhill" principle: heat moves from hotter to colder regions and energy dissipates unless you take measures to stop it (which involve a larger expenditure of energy elsewhere).
It is possible to force systems to absorb and keep energy by pumping energy into some kind of stable "storage" format inside the system. We do this when we recharge batteries, lift a book to a higher position on the shelf, or warm a cold drink in the microwave. A reaction does this by rearranging atoms into molecules with higher bonding energies.
Obviously, in nature, you are more likely to find exothermic or exergonic reactions that dissipate energy (give it off as radiation or increased motion) than you are to find endothermic or endergonic reactions that absorb energy, although the latter do occur.
Now, any given reaction can be written backwards: we can, in many cases, force the reaction to run in reverse by changing the conditions for the reaction such adding energy, or changing concentrations of one of the components. So the "arrow" for a given reaction doesn't tell us the direction of energy flow or the tendency of the reaction without further information. We can designate the direction of normal reaction by saying that it is product-favored (it will spontaneously produce the products at the end of the arrow if the reactants are available), or reactant-favored if it produces the reactants spontaneously.
Energy: forms and units
The study of energy is often considered as part of physics, but it is also a major conceptual consideration for chemists, who have to understand how heat or other forms of energy affect or are produced by chemical reactions.
There are two major types of energy. Anything which moves has kinetic energy; the amount of energy is proportional to the mass of the moving object and the square of its speed and is independent of the actual direction of its motion:
I do mean anything: gas molecules in motion, electrons in motion around the nucleus of the atom, and sound waves are all examples of motion, as well as cars and baseballs. Heat is a special form of kinetic energy--it is produced by the molecular vibrations in solids and the free motion of molecules in liquids and gases.
Anything which is restrained in a field of some kind has potential energy--energy of position. The amount of potential energy depends on the distance of the object from the source of the field, and on characteristics such as mass and charge. The primary force which concerns us in chemistry is electrical force; gravitational, weak nuclear and strong nuclear forces are the province of physics.
The electrons in molecules experience electrical forces from each other and from the positively-charged nuclei of the atoms in the molecule. These binding forces account for chemical potential energy. Objects with static charges such as ions and free electrons have electrostatic potential energy. In both cases, the amount of energy is related to the force on the charged objects according to Coulomb's law:
and the direction of the force is determined by the types of charge involved, according to the rule that like charges repulse one another and opposite charges attract each other.
As already mentioned (but this is important, so we'll say it again): regardless of the source or type, energy is always conserved. [This, by the way, is an absolute and not a statistical statement.] It can change form, from potential to kinetic energy, from chemical to heat to electrical forms, but it cannot be created or destroyed. Even the thermodynamic laws which are sometimes interpreted to mean that "the universe is running down" are concerned not with the disappearance of energy through some cosmic leak, but with the conversion of useful energy (which can do work, as defined by physicists) to useless energy, kinetic energy that simply drives particles to move in random directions with random speeds.
Normally in chemical reactions, we are concerned with the transfer of energy in the form of heat. Two major units are used to measure energy and perform calculations. The calorie (and kilocalorie) are derived from the original heat energy experiments of the nineteenth century, when the calorie was defined as the amount of heat necessary to raise 1 gram (or one milliliter or one cubic centimeter--they are all the same) of pure water from 14.5 to 15.5 degrees centigrade. The joule comes from kinetics experiments, and is defined as the kinetic energy of a 1.0 kilogram mass moving at 1 meter/second. The two are related by the conversion factor
Modern chemists express the heat energy of chemical reactions primarily in terms of kilojoules, symbol kJ, which is (obviously) 1000 J.
Specific heat capacity
Temperature is a specific type of heat measurement, and is an indication of the average kinetic energy of the items in some amount of mass in some state (solid, liquid, gas). Notice that to get from temperature to energy, we have to know how much mass is involved. It does not tell us the total heat available in a system; for that we need to know how much matter is at the average temperature.
Think of the differences between a sun-warmed swimming pool and a whistling tea-kettle full of boiling water. The temperature of the pool is lower than the temperature of the tea kettle, but the pool contains more heat than the tea kettle.
If you have trouble visualizing the difference, imaging the pool filled with dimes (representing the lower average kinetic energy of the individual water molecules) and the teakettle filled with quarters (representing the higher average kinetic energy of the individual water molecules). If what you are interested in is the total heat (the sum of the kinetic energy of all the molecules), would you rather have the pool of dimes or the teakettle of quarters?
Different substances can absorb energy (change temperature) at different rates, depending on the configuration of the atoms and molecules involved. The specific heat capacity of a given substance is defined as the amount of heat supplied (q, measured in Joules) divided by the mass of the substance (m in grams) and the actual change in temperature (ΔT in degrees K)
Because the ability of a substance to absorb heat is based on its structure, the heat capacity of a pure substance is a physical characteristic which can be used, once established, to determine the identity of a unknown substance, just as density can be used.
Changes of State
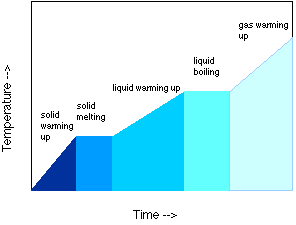
Energy is involved in changes of state, from solid to liquid to gas, of a pure substance, as well as in changes of temperature. To go from solid to liquid, chemical bonds holding the individual molecules together must be broken, and the reaction is endothermic, or energy-absorbing. The heat required for this change of state has a particular name, the heat of fusion. Likewise, a specific amount of energy, the heat of vaporization, is required to move a substance from liquid to gas state.
When a substance is changing state, it is not changing temperature; any heat added goes into the state change. So to determine the heat required for a substance to go from a lower temperature to a higher temperature through a state change, we must add up the energy required to raise the temperature from the start to the state change, the energy required for the state change, and the energy to raise the temperature from the state change to the final temperature. We have to consider both heat capacity and change of state.
As with the specific heat capacities, heats of fusion and vaporization are characteristic of a given substance. The heat of fusion of water is 333 J/g--that is, 333 J of heat energy are required to melt each gram of ice completely to a liquid state at 0 degC. The heat of vaporization of water is 2260 J/g. This is relatively high among liquids, and is an indication of the strength of the hydrogen bonds which form among polar water molecules in the liquid state.
Practice with the Concepts
Specific heat capacity
The heat capacity of aluminum is .902 Joules/gram-Kelvin, that of iron .451 J/gK. If it takes more energy to heat up a gram of aluminum than a gram of iron, why is aluminum a more common material for cooking pots than iron?
Discussion Questions
- Why must we consider the total mass of an object in determining its ability to absorb heat?
- Does it matter whether we use Centigrade/Celsius or Kelvin in measuring temperature differences? Why or why not?
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.