
Astronomy
The Main Sequence Stars

Weblecture
Stellar Evolution on and after the Main Sequence
Post Main Sequence Evolution
Much of what we know about stellar lifetimes based on their main sequence mass comes from the study of stars in clusters. Presumably, the stars in the cluster formed from the same clouds of material at roughly the same time, so they share similar characteristics except for their mass. By identifying stars in globular clusters (largely Population II stars which are metal poor and old, probably formed from the original hydrogen-helium clouds of the galaxy) and stars in open clusters (largely Population I stars, which are metal rich and forms from the detritus of supernovae), we can determine the age of the cluster, and compare the rates of hydrogen burnout based on the mass of individual stars.
Smaller Stars
In a small star, with a total stellar mass less than 0.4Mθ, thermonuclear fusion of hydrogen into helium occurs throughout the star. There is no identifiable core; as hydrogen in the interior of the stars consumed, convection circulation polls more hydrogen in, continually resupplying the thermonuclear activity with fresh fuel. Because of their low mass, the stars never achieve the pressure and temperature to burn very rapidly, so they appear as small, class M red stars, or red dwarfs. Because of their low rate of thermonuclear fusion, our best estimates indicate they would take dozens to hundreds of billions of years to reach hydrogen exhaustion. The universe is that old yet, so red dwarfs have not had time to reach their end-of-life (complete conversion to helium).
Medium Stars
A moderate size star with a mass between 0.4Mθ and 3Mθ will have a hydrogen-fusing core during its lifetime on the main sequence, which can last from 5 to 10 billion years. At some point, however, the supply of hydrogen in the core area drops to the point where thermonuclear fusion of hydrogen into helium can no longer be sustained. The core contracts, increasing pressure and causing it to radiate heat into the surrounding, still-hydrogen-rich layers above, which begin fusing hydrogen into helium, which "rains" into the core. Increasing temperatures cause the upper regions of the star to increase rapidly, which also increases the overall luminosity of the star. Expansion causes the surface temperature to drop, so while the amount of energy pouring out of the star is higher than when it was on the main sequence, that energy is emitted at a lower temperature and longer wavelength. The star becomes a red giant. The outer layers of gas are only weakly held by the gravitational field of this much larger star, so mass loss from the star also increases.
Meanwhile, in the core, the exhaustion of hydrogen fuel causes the core to collapse, increasing pressure and temperature. In the moderate mass star we are currently considering, this pressure is not sufficient however just poured helium fusion into beryllium. Instead, the core gases undergo a compression that separates atoms from their electrons, creating ions and free electrons. Since electrons cannot share the same quantum state, they exert pressure on each other, independently of the temperature of the core. Any situation in which subatomic particles exert such pressure in order to maintain unique quantum states is considered degenerate. In moderate mass stars, the core experiences a period of electron degeneracy, where only the pressure exerted by the electrons on each other prevents further gravitational collapse. However, this also limits the total pressure experienced by the core, so it fails to expand, it even when temperatures become high enough to trigger helium fusion. The increasing pressure causes the helium to ignite more and more quickly creating a helium "flash". The energy generated by the flash terminates the degenerate state of the core, and the star begins burning helium at a more normal rate.
Massive Stars
In high mass stars, the pressure at the core is high enough at hydrogen exhaustion for helium fusion to begin immediately. This heats up the still-hydrogen-rich shell above the core, so that it continues to fuse hydrogen into helium, which rains into the core, increasing the core mass along with supply of helium for helium fusion into beryllium. High mass stars never experience electron degeneracy states or the helium flash.
| Main Sequence Mass | Hydrogen Burning characteristics | Lifetime on Main Sequence | Hydrogen Exhaustion |
|---|---|---|---|
| Less than 0.4Mθ | Convection throughout star | Dozens of billions of years | No stars old enough to reach hydrogen exhaustion |
| 0.4Mθ to 3Mθ | Core hydrogen consumption | One to fifteen billion years | Helium ignition by flash after star core compresses to electron degeneracy. Star expands to red giant. |
| Over 3Mθ | Core hydrogen consumption | Several hundreds of millions of years | Helium ignites slowly; no electron degeneracy. Star expands to red giant. |
The life cycle of a mid-mass star can be summarized as a journey across the HR diagram.
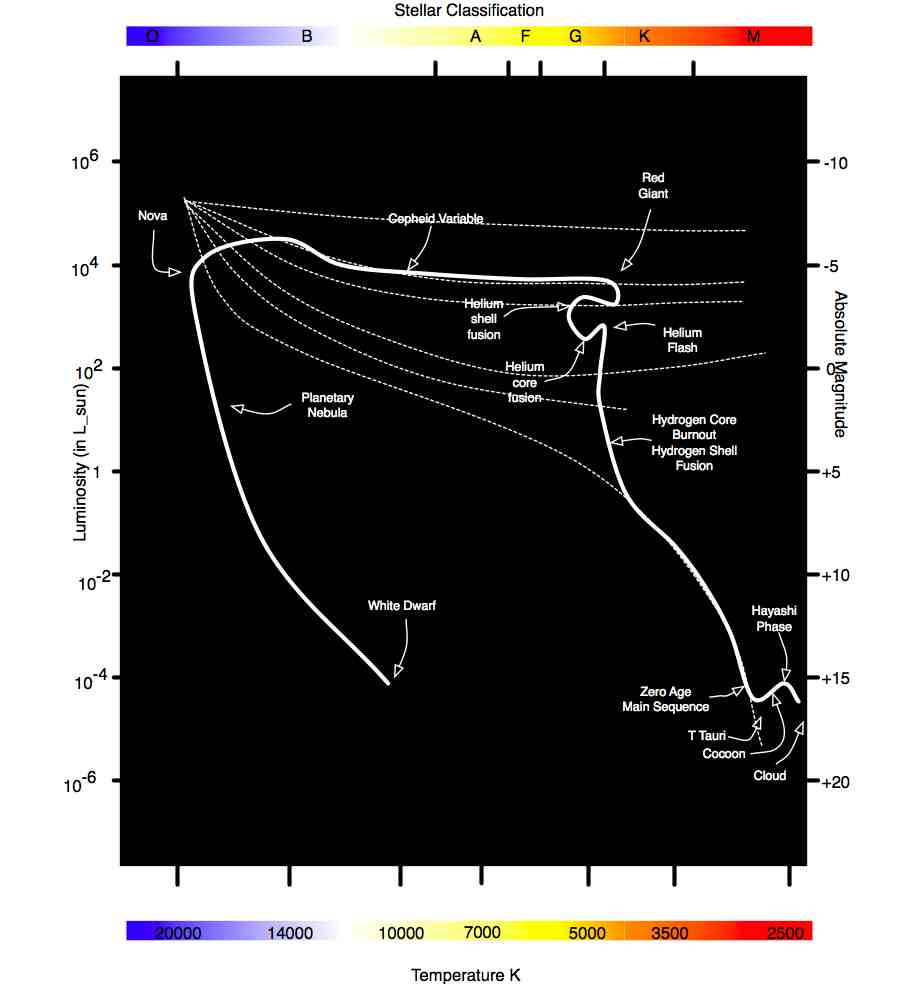
Variable Stars
There are two types of variable stars: stars whose magnitude changes because of periodic obstruction by another object, and stars whose magnitude varies intrinsically because of changes in the star. The first class, or optical variables, are often stars in binary systems where a fainter star orbits the primary and periodically eclipses it along the line of sight from Earth. The systems are useful for determining the mass of the stars involved and creating models which can be used to describe other binary systems.
All stars maintain a balance between gravitational collapse inward and heat pressure outward. Gravity constantly polls the mass of the star towards the center. However, the star doesn't collapse entirely, because the thermonuclear energy at its core generates heat energy, causing the gases to expand outward. The star doesn't simply blow up, however, because expanding gases cool off and begin to fall back into the star. So there is a constant expansion, cooling, and falling back cycle for any gas molecule near the surface of the star. This hydrostatic equilibrium allows stars to maintain a stable size over a long period of time.
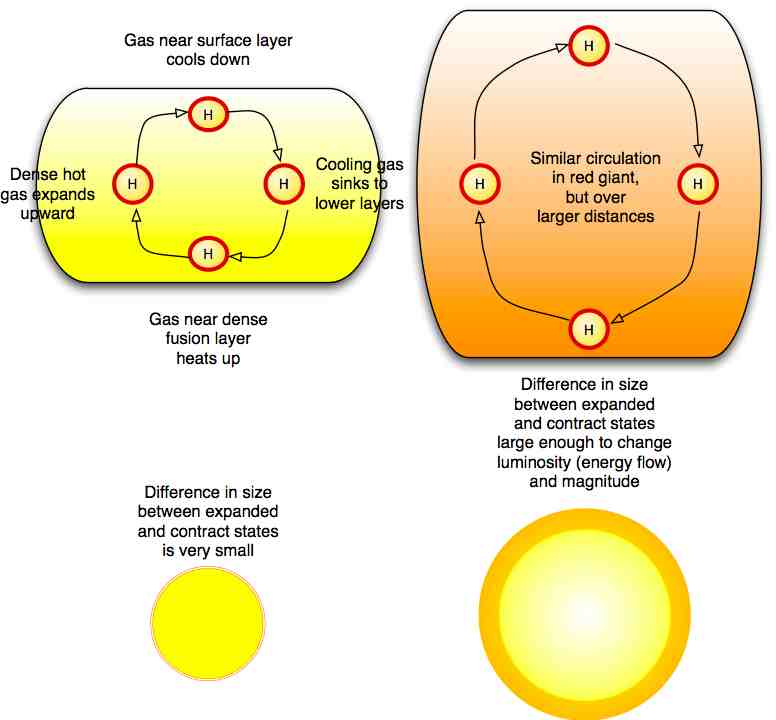
Two long-term variable types of stars have Period-Luminosity relationships. That is, the length of their periodic change luminosity appears to be a function of their average luminosity. With Cepheid variables, the lower the intrinsic luminosity of the star, the shorter the period. Type I Cepheid variables (population I metal-rich stars) have luminosities of about 103 times that of the sun when their periods are around one day long. Type I Cepheids with luminosities over 104 times that of the sun have periods that are over 30 days long. Type II Cepheids (population II metal-poor stars) have lower luminosities -- about 102.5Lθ for one day periods and 103Lθ for 30 day periods, but show the same kind of relationship.
RR Lyrae stars are lower-mass, metal poor Population II stars and have correspondingly lower luminosities, about 100Lθ.
It is easy to determine the length of the period from maximum to minimum of variable stars by direct observation. If we determine that a Cepheid variable Has a period of 10 days, and is a type II Cepheid (which we can tell from the lack of metal lines in its spectrum), then we know its intrinsic luminosity should be approximately 1000 times that of the sun. We can compare this with the apparent magnitude, and using the distance modulus, determine its distance. Cepheid variables become “standard candles” for measuring the distance to nearby galaxies, where because of their great brightness, they are easily identifiable. Since RR Lyrae variables are much fainter, we cannot use them to measure distance to galaxies. However, they appear in globular clusters with sufficient frequency that we can use them to map distances to the globular clusters in the halo around the Milky Way galaxy.
Binary Stars
Binary stars have interacting gravitational fields defined by Roche lobes. A particle on the line between the two centers of the stars will move toward one star or the other. But there is one point on the line where the forces of gravitation will be equal, the Lagrangian point. A particle at this point cannot move toward either star's center, because it is pulled equally by each star. Particles that are not on the direct line will be controlled by the star with a stronger gravitational field at that point.
As we've seen, a more massive star will burn more quickly and reach red giant stage sooner than a less massive star. In binary situations, the more massive star expands to fill the volume of space controlled by its gravitational field–its Roche lobe. Particles at the edge of the Roche lobe where it touches the lobe of the smaller star will begin to flow toward the smaller star. This creates a mass transfer, and over time it is possible for the smaller star to actually gain enough mass that it out-masses its once-larger binary partner. Location within a binary system can therefore change the expected lifecycle of a star.
Practice with the Concepts
Optional Readings
- Nick Strobel's Astronomy Notes site discusses the difference between giants and super giants, with a great diagram of the layers of a supergiant when it reaches iron-nickel stage.
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.