
Astronomy
Basics of the Solar System

Weblecture
Solar System
Our Solar System
Introduction
The Mars we had found was just a big moon with a thin atmosphere and no life. There were no martians, no canals, no water, no plants, no surface characteristics that even faintly resembled Earth's.
— Bruce Murray on the findings of Mariner 4, Journey into Space: The First Thirty Years of Space Exploration (1989).
Once Opportunity finishes its 91st sol, everything we get from the rovers after that is a bonus.
—Dr. Firoz Naderi, Mars Exploration Team at JPL, 8 April 2004, after Spirit completes sol 90 on Mars.
No signal from Opportunity has been heard since June 10, 2018. Opportunity likely experienced a low-power fault, a mission clock fault and an up-loss timer fault. The team has been listening for the rover over a broad range of times using the Deep Space Network (DSN) Radio Science Receiver since loss of signal. In addition, more recently they have been commanding "sweep and beeps" throughout the daily DSN pass to address a possible complexity with certain conditions within mission clock fault.
—JPL Status Update, sol 5111 mission as of October 22, 2018.
The Nine Planets
We will be studying each of the planets in detail. As we look at them, we want to try to find patterns in different areas. In this weblecture, we list the main topics of planetology, and look at a few in detail, starting with rotational and orbital characteristics, and some observations about comparative mass and size and their application to a planet's retention of an atmosphere.
Orbital characteristics
- Maximum, minimum, and average distance from the sun -- there appears to be a pattern, but we can't explain it (the Titus-Bode relationship).
- Orbit eccentricity -- There does not appear to be a pattern.
- Orbital speed -- Planets further from the sun travel more slowly. As Kepler noted, planets with eccentric elliptical orbits move more quickly when they are near perihelion then when they are near aphelion points.
- Orbital period -- Planets further from the sun have longer periods, in a predictable fashion. Kepler's second law relates period P to the semi-major axis distance from the sun a: P2 = a3. Newton's law of gravity and the rules for circular orbit speeds explain why this relationship must hold for all objects in orbit around a primary mass, not just planets orbiting the sun.
- Inclination of orbit to ecliptic -- There does not appear to be a pattern.
The Titius-Bode Relationship
An empirical law is a relationship based on patterns which have been observed, but for which no causal explanation (in terms of natural forces) has been found. The law is the result of pure observation, not derivation from general principles. A good example of a currently unexplained empirical relationship is Bode's law, which relates his observed distances of the planets from the sun to a mathematical relationship. In the table below, an AU is an anstronomical unit, the distance between the earth and the sun. We start with a primary factor (.3AU) and the value 0, to which we add a secondary factor (.4AU) to get the distance to Mercury (.4 AU). We then use 1 times the primary factor .3AU, add the secondary factor .4AU, and get the distance .7AU to Venus. From this point on, we double the primary factor each time (.3AU, .6AU, 1.2AU, 2.4AU....) , and add the secondary factor (.4AU) each time to get the distances to succeeding plants.
When Jahann Titius and Johane Bode first reported this relationship around 1766-1768, there was no planet for the predicted distance of 2.8 AU (between Mars and Jupiter) or at 19.6AU. In 1781, however, William Herschel's discovery of Uranus filled the slot for one of the planets with a distance of about 19.2AU. Then in 1800, the Italian astronomer Giuseppe Piazzi discovered Ceres, the first of thousands of asteroids, and determined that its distance matched that predicted for the missing planet between Mars and Jupiter.
| Planet | Distance from sun (in A.U) | Titius-Bode Relationship | Predicted distance |
| Mercury | .39 | .4 | |
| Venus | .72 | .4 + 1 * .3 | .7 |
| Earth | 1.0 | .4 + 2 *.3 | 1.0 |
| Mars | 1.52 | .4 + 4 * .3 | 1.6 |
| Asteroids | .4 + 8 * .3 | 2.8 | |
| Jupiter | 5.2 | .4 + 16 * .3 | 5.2 |
| Saturn | 9.5 | .4 + 32 * .3 | 10.0 |
| Uranus | 19.2 | .4 + 64 * .3 | 19.6 |
| Neptune | 30.0 | ||
| Pluto | 39.4 | .4 + 128 * .3 | 38.8 |
Some astronomers believe the mathematical pattern in distances is a simple coincidence, but others believe it might be a kind of orbital resonance that occurs during the condensation and formation of a star, and characteristic of any stable orbital system. If so, then other solar systems will display the same type of pattern. A further speculation is that where a local pattern is violated (as in the case of Neptune and Pluto, where Neptune is much closer to the sun than predicted), the deviation may point to a past catastrophic event, such as a collision or near-miss situation.
Rotation and axis
- Rotation periods -- Gas giants rotate more rapidly than terrestrial planets.
- Incination of equator to orbit (axis tilt) -- There does not appear to be a pattern.
- Orbital direction -- Planets move counterclockwise around the sun if viewed from a point above the Earth's north pole.
- Rotational direction -- Most planets rotate counterclockwise if viewed from the same point above the Earth's north pole. Again, the deviation of Venus and Mars from this pattern may indicate past catastrophic events.
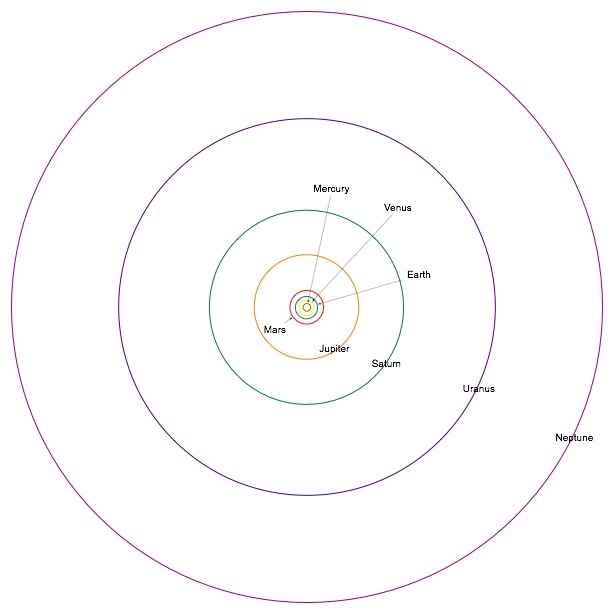

Seen from the top, the orbits of the planets are nearly circular. Seen from the side, they appear to lie in a single plane, like the rings around Saturn.
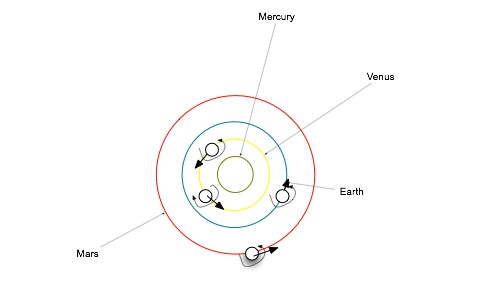
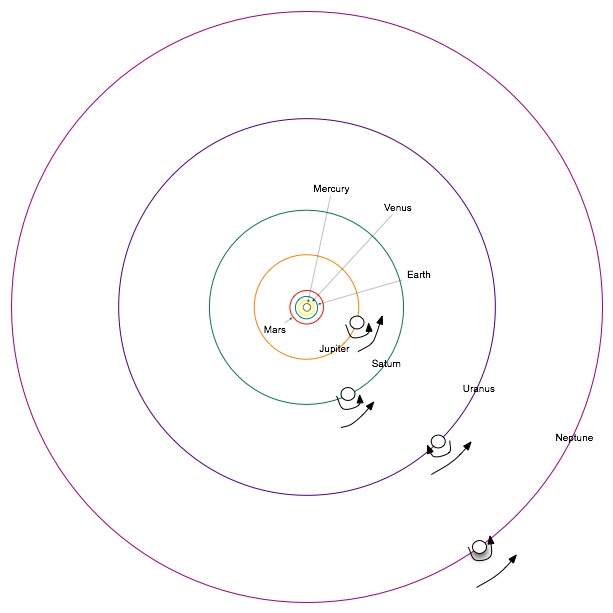
The planets revolve around the sun in a counter-clockwise direction if viewed from high above the earth's north pole. Most of the planets also spin on their axis in this direction, but Venus and Uranus are technically in retrograde rotation.
Physical characteristics
- Diameter -- varies; gas giants are much larger than terrestrial planets.
- Mass -- varies; gas giants are much greater than terrestrial planets.
- Density -- terrestrial planets have higher densities than gas giants.
- Escape velocity -- depends on diameter and mass.
- Surface gravity -- depends on diameter and mass.
- Albedo -- depends on surface composition.
- Surface temperature -- depends on distance from sun.
- Internal structure (core, mantle, crust, etc.) -- varies; terrestrial planets are more complex than gas giants.
- Composition -- gas giants are mostly light elements; terrestrial planets are heavier.
- Geological activity -- depends on core composition and gravitational stress.
Comparison of physical characteristics of solar system objects is a relatively new science, planetology, made possible by the unmanned exploration of solar system objects in the last half-century, particularly the Viking Lander and Orbiter missions to Mars in the 1970s, and subsequent orbiting and rover-class missions in the last decade, the Voyager missions to the outer planets, Galileo and Cassini at Jupiter, Mariner 10 and Messenger to Mercury, the Venera (USSR) and Magelllan missions to Venus. These missions have allowed us to detect general similarities and puzzling differences between the planets, and have led to a new classification of solar system objects, one which is still controversial and struggling to recognize patterns in inherent physical characteristics as well as location around another object, or at some distance from the sun. One critical issue is the third criteria, since it could be argued that Earth has not "cleared its neighbor", given there are nearly 10 000 near-Earth asteroids. Also at issue is the applicability of the defintion: of the more than 9000 members of the IAU, less than 2800 attended the conference, and only 424 votes were cast to approve the new classification system. Nevertheless, the practical ramifications were felt immediately: subsequent editions of all astronomy texts had to be rewritten to reflect the removal of Pluto from the list of "planets".
| Classification | Definition | ||||||||
| Planet | In the final definition passed by the IAU August, 2006, a planet must fulfill three criteria:
Only Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune fulfill all three criteria. A quick look at the other points of planetary characteristics will show two subcategories: the small, dense planets near the sun called terrestrial planets because of their Earth-like qualities, and the large, mostly hydrogen and helium gas giants, which lie beyond the asteroid belt. |
||||||||
| Dwarf Planet | A dwarf planet fulfills the first two planetary criteria, but has not cleared its local orbital area of other similar massive objects. Dwarf planets include Ceres (in the asteroid belt), Pluto, Makemake, Haumea (in the Kuiper Belt) and Eris (in the scattered disk region). | ||||||||
| Small Solar System Body | SSBS are irregularly-shaped objects which do not meet either the second or third planetary criteria, but do orbit the sun. These include all asteroids and most trans-Neptunian objects in the Kuiper Belt, scattered disk, and Oort Cloud.
|
||||||||
| Trans-Neptunian Objects | |||||||||
| Kuiper Belt Objects | The Kuiper belt is a toroid (doughnut-shaped) region extending from the orbit of Neptune out to about 55AU from the sun. It contains three dwarf planets (and probably many more) but is primarily made up of small asteroid-like bodies. From the approximately one thousand known Kuiper Belt objects, astronomers estimate that around 70 000 objects at least 100km in diameter exist in this region. | ||||||||
| Scattered Disk Objects | SDOs have high orbital exccentricities and inclinations - they loop out of the solar system disk. Most have perihelion distances around 30AU, but can have ahelion distances up to 100AU. As with the Kuiper Belt, there are a few dwarf planets, but most objects will be asteroid-like. Around one hundred SDOs have been identified, including 2007 UK126, Eris, and Sedna; best estimates are that the number of 100km objects is roughly equal to that in the Kuiper Belt, although far more widely scattered. This region is thought to be the origin of most periodic comets. | ||||||||
| The Oort Cloud | A still-hypothetical spherical cloud of comets with distances up to 1 light year from the sun. Objects within this area are held within the Sun's gravitational field. Three objects, 90377 Sedna, 2000 CR105, and 206 SQ372 are currently the only candidates for Oort Cloud membership. | ||||||||
| Natural Satellites | These include all natural bodies that orbit one of the solar system bodies defined above, but do not directly orbit the sun. Note that a number of bodies would be planets in their own right if they orbited the sun, and many more would be dwarf planets. | ||||||||
Atmosphere
Not all planets have atmospheres. A planet can retain a light gas molecule only if its temperature is low and its mass is high enough that the escape velocity of the planet is greater than the average velocity of the gases around it.
The velocity given by the gas temperature's average kinetic energy is an average: some molecules will have higher velocities, some lower. If a planet has an escape velocity equal to the average gas molecule velocity, half the gas molecules will escape! So the escape velocity for a planet must be significantly higher than the average velocity of a gas molecule for the planet to retain an atmosphere containing that gas. The rule of thumb is that a planet can retain an atmosphere if vescape = 6 vmolecule.
- Composition -- varies with mass and surface temperature of planet (determines planet's ability to retain gases).
- Temperature -- varies with composition of atmosphere (greenhouse effect raises temperature).
- Density -- varies with composition and mass of planet.
Temperature drives the molecular velocity of gas molecules. The average speed of a gas molecule is
The escape velocity for the same molecule is
If we put these two together, we get a relationship that if
a molecule m will have escape velocity and be able to leave the planet's gravitational field. Consider an oxygen molecule (O2, mass = 5.32 * 10-26 kg) in the Earth's atmosphere. At 20 °C (293K), it's average velocity is 0.478 km/s -- far below the 11.2 km/s escape velocity required by Earth's mass compressed into its volume. For an oxygen molecule to escape Earth, the temperature of the atmosphere would need to be
or 121080K -- hotter than the surface of most stars! On the other hand, the mass of H2 is so low that it constantly escapes Earth's atmosphere.
Unique surface features
- Impact craters from meteor and asteroid strikes.
- Mountains, rills, rifts, scarps, and volcanoes caused by tectonic stresses.
- Polar caps and ice floes resulting from surface water erosion processes.
Practice with the Concepts
Discussion Questions
- Look at the orbital data for the planets in Appendix I of your text.
- What kinds of data do astronomers record about planets? What kinds of information can we logically deduce or assume from this data?
- Why does the synodic period of the inferior planets differ from that of earth so much? Why is the synodic period of the outer planets nearly the same as earth's year?
- If you have a spreadsheet, chart the semimajor axis in AU against the sidereal period in years. Is the curve a straight line? Why?
- Which planet has the greatest orbital eccentricity? How does this affect conditions on the planet? How does this affect observations of the planet from earth?
- Which planet has the greates inclination to the ecliptic? How does this affect conditions on the planet? How does this affect observations of the planet from earth?
- What is the evidence cited for the current model of the formation of the solar system? What are the problems with this model, if any?
Optional Webreading
- Take a look at The Nine Planets website, which has tons of information.
- The NASA Planetary Pictures site has pictures from the American efforts to explore the solar system. The actual exploration page at NASA Solar System Exploration has information about current and past missions.
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.