Telescope Basics

Telescopes, Optics, and Lenses

• Introduction
• Telescopes
• Amateur Observing
• Practice with Concepts
• Discussion Questions
• Optional Website Reading

Introduction

Telescopes

Lenses and Geometric Optics

Long before Galileo attempted to put two pieces of curved glass together to create a telescope, the Greeks and Arabics described the behavior of light rays through lenses and as reflections from mirrors. Polished crystal lenses had been known since Babylonian and Egyptian times, and the Romans and Greeks used spherical glass balls filled with water as lenses, but polished glass lenses are a product of more recent Arabic and Medieval craftsmen. The mathematician Euclid wrote a text on optics that described the reflective and refractive behavior of light rays, without explaining their physical nature. The Arabic philosopher Ibn al-Hatham is often called the "father of modern optics", since he not only formulated rules of reflection and refraction but demonstrated them experimentally. He rejected earlier theories that light proceded from the eye and insisted that it came from the light source (primary light, or was reflected by a non-emitting surface (secondary light). He developed mathematics to show how light was reflected from a curved mirror as well and built a camera obscurato show how a small pinhole can act like a lens to focus a light source on a screen, but with the imag upside down.

We can summarize the rules of geometric optics in modern terms. If we look at a plane (flat, straight) surface on a dense medium, we can draw a line perpendicular to the medium: this line is the norm. Light striking the plane surface at angle Φ₁ will leave it with an angle Φ₂ of the same magnitude. Light entering the dense material bends towards the norm, creating the smaller angle Φ₃. Light leaving a dense material bends away from the norm. The reasons for this are beyond the scope of this course, but it is worth noting that light travels more slowly in a dense medium. The rule that the speed of light gives the upper limit for how fast anything in the universe can travel refers to the speed of light in a vacuum.

By choosing our medium and curving the surface properly, we can cause all the light passing through our object or lens to bend in such a way that it focuses at a single point (convex lens) or disperses away from the point at which it enters the medium (concave lens).

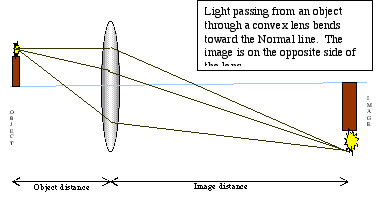
The image produced by the convex lens is a real image: if we put a screen at that position, the light focussed on the screen produces a picture we can see (this is how projectors work). The light rays spreading out from a single point on the object are bent differentially by the lens and converge at a single point, creating the image. The distance of the object from the lens, the curvature of the lens, and the distance of the image from the lens are interdependent, and given by the thin lens rule (sometimes called the "lens maker's formula"):

1/f = 1/d_o + 1/d_i

In this formula, the value f is the focal length of the lens, the distance at which parallel lines entering the lens are focussed to a single point. If you have ever used a lens in sunlight to start a fire, you've demonstrated the focal distance of the lens.

Convex lenses have surfaces that curve outward from the center; they are thicker at the center than at their edges. Concave lenses curve inward: they are thinner at the center than at the edges. This "inverted" curvature causes light rays passing through the lens to disperse rather than converge at a point.

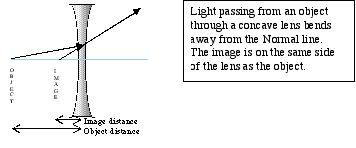
The image produced in this case by the concave lens is virtual: we look through the lens toward the light source to see the image. Since we are looking at the result of the light bending process of the lens, no light ray actually comes from or passes through the image we observe.

Concave lenses also use the thin lens rule. As with convex lenses, the distance from the object to the lens is the object distance; the distance from the image to the lens is the image distance. The object distance is always positive. For the image distance, we have to pay attention to its location relative to the lens: the image distance is positive if it is on the same side of the lens as the object (concave lenses) and negative if it on the far side of the lens (convex lenses).

Magnification

Magnification is determined from the relationship

$$M=-\frac{d_i}{d_o}$$

The minus sign on magnification indicates that the image is inverted; since d_o is always positive, the inversion will depend on the value and sign on d_i.

By increasing the size of the lens or mirror, we increase the light gathering power of the telescope. The observed brightness depends on the total surface area of the mirror, which is pi*d²/4, where d is the diameter. This brightness diminishes over the distance to the focal length according to the inverse square law, so brightness is proportional to d²/f².

Resolution

The resolving power of a telescope is its ability to separate two close images. This is a function of the magnification of the telescope, but also of its diameter. Remember that light passing near an edge is diffracted, cause the light to bend. The opening of the telescope acts like a double slit, and an interference pattern results, with "bright" and "dark" areas. The larger the diameter of the telescope, the greater the resolving power. If we measure the diameter of the telescope in centimeters, then the maximum angular separation in seconds α is given by $$\alpha =\frac{11.6}{D}$$

For a 10cm telescope, the maximum angular separation is 11.6/10 = 1.16 seconds of arc. Any two objects with a smaller angle of separation will appear as one blob in the telescope.

Telescope combinations

A telescope combines two or more lenses to produce a virtual image the viewer sees at increased magnification (and upside-down).

The distance from the main lens on the left (the objective) to the real image is the focal length of the objective, f_o. The distance from the eyepiece lens on the right to the virtual image is the focal length of the eyepiece, f_e. The magnification of the telescope is M = f_o/f_e.

A number of problems face the astronomer putting together a double lens telescope. Lenses do not refract all colors of light equally; the light is spread out and focuses in different points. This chromatic aberration can be reduced by using lenses of different refracting capabilities. The combination is called an achromatic lens.

Similar problems attend the use of mirrors. The easiest mirrors to make are spherical mirrors, but parallel rays striking the mirror at different points focus at different distances, dimming the image. To get around this, most telescope mirrors have a parabolic curvature. While this fixes spherical aberration, it results in a coma or haze effect when non-parallel light striking the mirror is focussed to different points.

While achromatic lenses produce the finest images, it is very difficult to manufacture and support large glass pieces. Mirrors, on the other hand, can be supported from behind. Moreover, they allow us to bend the light back and forth, reducing the overall physical size of the telescope. An observer can stand comfortably, or better yet (for scientific purposes), place film, a spectroscope, or a charge-coupled device (CCD) at the focal point to collect the light information coming into the telescope. The different types of recording devices provide for the observation of light energy outside of the visible spectrum.

Most advanced observation is done these days by very large telescopes using CCDs, arrays of telescopes placed strategically on the earth's surface, or by telescopes in space, where weather conditions, pollution, and filtering from the atmosphere can be eliminated. Astrophotography is still pursued by amateurs, many of whom do spectacular work.

Reflectors

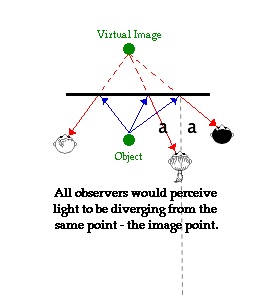	Snell's law explains how light reflects from a surface. In a plane mirror, the angle of reflect = the angle of incidence rule allows viewers at different angles and distances to perceive a virtual image in the same apparent location.
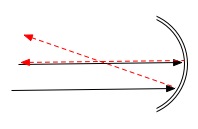	We use a "normal" ray into the center of the spherical mirror as a reference; this ray hits a surface that is perpendicular to it, so that it is reflected directly back on itself. Other light rays entering parallel to our reference ray but at the same distance from the center hit the mirror at the same angle, and are reflected back at an equal angle to the normal, following Snell's law.
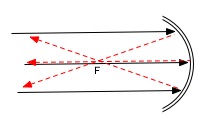	Because of the curvature of the mirror, all the parallel rays wind up passing through the same point, or the mirror's focal point.
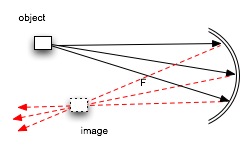	When rays from the same source strike the interior or convex surface of a spherical mirror at different points, the difference in reflection angles forces the rays to converge, creating a real image, on the same side of the mirror as the object.
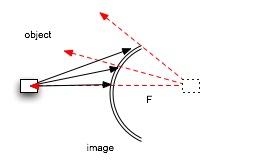	When such rays strike the external or concave surface of the mirror, they are sent in divergent directions. The image apparently lies within the mirror.

Spherical mirrors are fairly straightforward to make, but they do have several problems that affects their function. One is spherical aberration, which results when parallel rays at different distances from the center converge toward their focal points. These points will differ slightly, depending on the distance (and angle) of the surface point from the center of the mirror. The resulting image is blurred. This problem is usually resolved by using a parabolic mirror rather than a perfectly spherical mirror: this fixes the issue with rays of light striking the edges of the mirror, but introduces a new defect (coma), where rays near the center are deflected differently. Most modern reflector telescopes use coatings or mirror-and-lens combinations to reduce coma effects.

Reflector telescopes have one huge advantage over refractor telescopes: we can make them much, much larger, supporting the mirror base at the low end of the telescope (instead of putting a large heavy objective lens at the least-supported upper end of the telescope), and even folding light back and forth between a primary and secondary mirror to increase the effective focal length of the telescope without increasing its actual size.

Amateur Observing

Amateur astronomical observers are responsible for many discoveries, particularly of comets and asteroids. While professional and academic astronomers may have access to larger telescopes and better computers, they often lack the time necessary for continuous surveys of the same region of the sky -- the kind of observation necessary to spot new phenomena, such as nova, supernovae, or comets.

Simple small telescopes can still teach you a great deal about how an astronomer works (not to mention giving you the thrill of seeing craters on the moon, the changing positions of Jupiter's moons, or Saturn's rings with your own eyes). Both refracting and reflecting telescopes are available to amateur observers.

Refractors

---

Reflectors

Practice with the Concepts

You are able to look through a 6-meter and a 10-cm diameter telescope. Which gives a brighter image of the same star?

What is the resolving power of the 6-meter telescope?

What is the magnification of a telescope whose main object if has a focal length of 1.5 meters if you use an eyepiece of 35mm?

Discussion Questions

• Do most professional astronomers actually look through their telescopes? Why or why not?
• Explain the advantages and disadvantages of refractors vs. reflectors.
• Explain the advantages and disadvantages of telescopes sensitive to γ-ray, UV, IR, and radio wavelengths compared to visible light.
• Explain the advantages and disadvantages of Earth-based vs. space-borne telescopes.

Optional Readings

• For the current list of orbiting telescopes, check the current WIKI list.
• The Hubble site has information about the telescope, its current state, and Gallery pages.
• The James Webb Telescope site has the latest pictures from the Webb Infrared Telescope.

---

© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.