The Nature of Light and Matter: Radiation

Determining the Nature of Light

• Introduction
• Electromagnetic Radiation and How It Helps Us Figure Out What Is Going On In Space
• Practice with Concepts
• Discussion Questions
• Optional Website Reading

Introduction

Until the 1960s, man was unable to touch the moon or other planets. Everything we knew about planets, and even now, everything we know about stars comes through the medium of light. Because of the way matter generates light, we can tell something about the level of energy (including temperature) and the composition of a light-emitting source. Because of the way light travels through space, we can tell something about the distance and motion of the light-emitting source. We'll start by looking at the nature of light itself, and how the temperature of a source influences the color of light it emits.

Electromagnetic Radiation and How It Helps Us Figure Out What Is Going On In Space

Speed of light

The inability to time experiments accurately hampered Galileo's efforts to determine the speed of light because he was working before the invention of a reliable clock, and the distances over which he could send a controlled beam were relatively short. Roemer's determination of the speed of light from observations of the moons of Jupiter were possible only because the distances involved were large enough to make the differences between predicted events and observations of the event noticeable. Fizeau-Foucault's method has been the most reliable method, and modern measurements still rely on experiments that use coherent beams of light (LASERS, usually), and rapidly rotating mirrors.

Because of its accuracy, Michelson and Morley used this system of light beams and rotation mirrors to attempt measuring the rate of speed of the earth through the "ether" that they believed filled all of space by measuring the difference in the speed of light when sending light in the direction of the earth's motion and at right angles to it. This resulted in the most famous experimental failure of all time, because they detected no difference! Ultimately, they had to conclude that not only was there no ether, but that the speed of light was constant regardless of the motion of its source, a point of data which Einstein explained in his theory of relativity. We'll come back to this result when we discuss the implications of relativity for stars of enormous mass that collapse to black holes.

The wave nature of light

Electromagnetic radiation is simply a form of propagation of energy through space, usually from a point source. Isaac Newton conceived of light as small particles that moved through space; different colors had different properties. However, Christaan Huygens thought of it as a form of wave. Experimental evidence to support Huygen's theory was supplied by Thomas Young's double slit experiments, which showed that light going through a pair of narrow slits produces a diffraction pattern similar to that of waves in water passing through similar barriers.

You can create create this effect by looking with one eye at a light source (a room or table lamp is sufficient) through the slit produced by holding your fingers close together and close to your eye. You should be able to see one or more dark lines alongside the actual edges of your fingers. These are the minima (equivalent to still water) where light waves striking each edge of the slit are diffracted and interfere with one another.

James Clerk Maxwell put observations by Auguste Coulomb, Andre Ampere, and Michael Faraday together to create a coherent picture of electromagnetic radiation. Coulomb's rules explained that two electrical charges worked like two masses. Where two masses experience an attractive force proportional to the masses and inversely proportional to the square of the distance between them, two charged particles have a force (whether it is attractive or repulsive depends on the type of charge) proportional to the charges and inversely proportional to the distances. Ampere noted that current in wires resulted in magnetic forces. Faraday was able to show that changing magnetic fields cause electric current to flow. Maxwell realized that only when charges are static (not moving) are they without magnetic effect, but that a changing electric field will generate a changing magnetic field, that can in turn generate a changing electric field. Such a phenomenon would be a self-propagating wave (see diagram on page 104). When Maxwell calculated the speed of the wave, he realized that it coincided with the speed of light, and concluded that the self-propagating wave was light.

The frequency and wavelength of any wave (light, sound, water waves) are related by the formula c = λ * ν, where c is the speed of the wave, λ is the wavelength or distance between successive peaks, and ν (sometimes f) is the frequency, or number of peaks passing a given point per second. The longer the wavelength, the fewer the number of peaks passing a given point, so the lower the frequency. We say that frequency and wavelength are inversely related: λ = c/ν and ν = c/λ.

Blackbody Radiation

Since the light emitted by an object is affected by its temperature, we also need to make accurate observations of temperature. Temperature is a measure of the average kinetic energy, or energy of motion, of all the particles. We measure this using one of three scales: civilians use the Fahrenheit scale, but chemists, physicists and astronomers use either the Celsius scale or the Kelvin scale. The centigrade scale has degrees calibrated so that the difference between the freezing and boiling points of water is 100 degrees, and sets the zero point at the freezing point of water. The Kelvin scale uses degrees of the same size, but the zero point on the Kelvin scale is the theoretical temperature at which volume goes to zero if pressure on a normal gas were infinite. At this point, gas molecules shouldn't be moving any more, and with zero velocity, they have no kinetic energy. On the Kelvin scale, the zero is absolute; there is no colder temperature that has any meaning.

We can relate the color of light to the temperature of a dense object by looking at the colors or spectrum emitted by a dark, pure substance (such as iron) in the shape of a sphere. Such an object comes close to absorbing, rather than reflecting, all the light falling on it, so it is called a blackbody. We heat the sphere up and watch the intensities of different parts of the spectrum change with temperature. Obviously, a blackbody will emit light over a range; it isn't a laser. But the wavelength at which most of the light is emitted—the peak wavelength, because a peak marks it on a chart of wavelength vs infinity)—increases in frequency. The pattern can be generated by a mathematical law called Wien's law, which says that wavelength * temperature = a constant. If we measure the wavelength in meters and the temperature in kelvin, this constant has the numerical value of 0.0029.

We can now use this relationship to relate the temperature of the body to the total light it puts out. We measure the flow of energy through a given area as the flux of energy. From work done by Stefan and Boltzmann, we can relate the flux of a fixed portion of the blackbody's surface (say one square meter) to its temperature: $$F=a\mathrm{constant}\ast T^4$$

The constant is usually noted by the Greek letter σ (sigma). The luminosity of a body is the total flux of energy through the whole surface area of the body. For a sphere, the surface area is 4 * π * R², so the total luminosity can be expressed this way:

luminosity = flux * surface area $$\begin{array}{l}\\ L=F\ast 4\pi R^2\end{array}$$

We can rearrange this to express flux as a function of luminosity: $$F=\frac{L}{4\pi R^2}$$

and since flux shows up in Wien's law, we can set the two expressions equal to one another: $$\frac{L}{4\pi R^2}=F=\sigma T^4$$

So, if we know the luminosity, we can figure out the temperature of the blackbody.

Spectroscopy

One of the results of these studies was the realization that different elements produce different spectra, and that the spectrum of an element can be used to identify the element.

How do we actually look at a spectrum? Most astronomical instruments use a diffraction grating, which is a set of very close, very fine lines on a transparent film that causes light passing through it to spread out, just as it would going through a spectrum. When the film is attached to a tube with a single slit, the diffraction of the slit and the spreading process of the diffraction grating allow us to look at the individual colors produced by a glowing light source — a star, a very hot spherical metal ball acting as a black body, or, as in this case, a standard household fluorescent bulb.

The viewer looks through the diffraction grating to see the individual lines created by the light source "floating" inside the tube.

By adjusting the tube and light source, the view can see many lines emitted by the excited electrons in the gas sample of the fluorescent light. Notice how close together the red and yellow lines appear in this photograph.

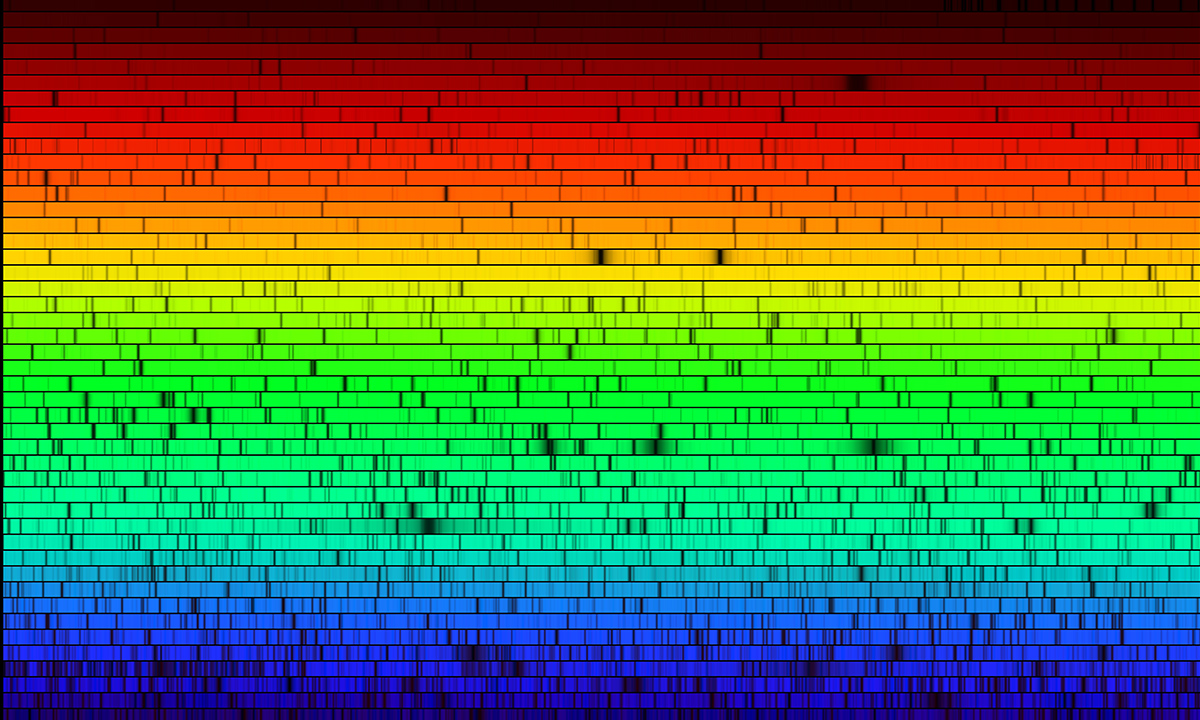
NASA solar spectrum. Notice the dark band in the red -- that's the helium α band.

Practice with the Concepts

Discussion Questions

• How many different kinds of information can we determine about stars from the light we see coming from them?
• What would happen to our above conclusions if the gravitational constant varied? If energy were not dependent at the same level on wavelength throughout the universe?

More: Optional Readings

• Decoding Cosmic Spectra is based on a Nova presentation.

© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.