Astronomical Methods and Tools

Astronomy and the Universe

• Introduction: The Study of Nature
• Tools of Science
• Practice with Concepts
• Units in Astronomy
• Discussion Questions
• Optional Website Reading

Introduction: The Study of Nature

The Tools of Science: Mathematical Tools and Notation

We start our study of astronomy by identifying some of the things we will study, and some of the tools we will use. Astronomers have over the centuries developed a number of terms and methods which have very precise meanings, so part of learning science is learning to write in a new kind of language about these things.

Angular Measurement: One of the tools of astronomy

If you are not comfortable with angular measurement, you may want to practice a little with the concepts, angle sizes, and the actual sky.

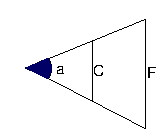
We always look at the sky as if we are at the bottom or apex of the angle (a) and the two things we measure are at the far points of each side. Note that two "close" objects can have the same apparent angular distance as two "far" objects, but be much closer together (distance C) physically than the far objects (distance F). In order to determine the actual physical separation, we must know both the angular separation and the distance to the objects.

A 360-degree circle breaks into four 90-degree parts. Ninety degrees is the distance from any point on the horizon to the point directly over your head. Ninety degrees is also the distance from the celestial equator (any point in the sky directly above the earth's equator) and the celestial north pole (the point directly above the earth's north pole), currently near the star Polaris in the Little Dipper.

The 360-degree circle also breaks into 24 15-degree parts. If the sky rotates once in 24 hours, then it must move 15 degrees in one hour. If your hand is a "normal adult hand" like the one in the text, then it is about 10 degrees across the palm, so a star on the eastern horizon at 9pm at night will be one-and-a-half palm widths above the horizon at 10pm. The twelve constellations known as the signs of the zodiac that lie along the celestial equator are each 30 degrees across. Knowing these "rules of thumb" will help you keep time by the stars and navigate to those you want to observe.

Scientific notation: Expressing numbers easily and accurately

If you have not worked with scientific notation before or done such calculations on an electronic calculator, work carefully through the examples, and dig out the manual that came with your calculator to help you. Study the terminology on p. 15 so that you can quickly convert "million" to "six zeros" or "10⁶". Study the manipulation of exponents in box 1-3. You can get the order of magnitude of an answer quickly if you remember that you add exponents that are multiplied together (10³ * 10⁴ = 10⁷ because 3+4 = 7) and subtract exponents that are divided (10⁵/10³ = 10² because 5 - 3 = 2). Pay attention to those negative signs on exponents as well (10^-5/10³ = 10^-8 because -5 -3 = -8)!

Units: Relating abstract numbers to reality

All scientists rely on units, because what we measure is not pure number but some dimensional thing: length (in meters), mass (in grams), light intensity (in candles!), energy (in ergs), temperature (in degrees centigrade), and so on. When we convert quantities to different units, from miles/hour to kilometers/second, for example, we have to account for the change from hours to seconds and the change from miles to kilometers. When we calculate derived quantities such as density (mass/volume) which cannot be directly measured, we must also specify the units. Any conversion or calculation that involves measurement involves units that must be specified and tracked.

Astronomers use their own units, because the sizes involved are so large. Like any other science, when you need to convert from one unit to another, keep the unit names around and cancel them out just like you would cancel the numbers.

Why do we bother with different units? One reason is that the proper units let us easily compare certain kinds of information. For example:

• an astronomical unit is the distance from the earth to the sun. When we say that earth is 1 AU from the sun, but Jupiter is 5.2 AUs from the sun, we mean that Jupiter is a bit more than five times as far from the sun as earth. In situations where some effect of the sun depends on distance, using astronomical units makes it easy to compare the result at any planet. Light intensity diminishes as the square of the distance, so amount of light reaching Jupiter will be 1/5² = 1/25 of the light reaching earth.
• a light year is the distance light travels in a year. If we convert distances to light years, we know how long ago the light we see now left its source. The star Vega in the constellation Lyra is about 25 light years away. When you find Vega in the sky, you see it the way it was a quarter of a century ago, probably before you were born.

Practice with the Concepts

Scientific Notation

Scientific notation involves two important concepts. One is significant figures, and the other is order of magnitude. Scientific notation eliminates some of the ambiguity for each of these.

The significant figures in an number are the digits that have actual scientific meaning and are not just placeholders. Error is assumed to be limited to the smallest place containing a significant figure. The tricky part of this is zeroes.

• Zeroes to the right of non-zero digits but to the left of the decimal are assumed to be just placeholders.
• Embedded zeroes are significant, even though they are just placeholders, because they give meaning to the numbers on either side.
• Zeroes to the right of the decimal place are significant, however—otherwise, why bother writing them?

In the number 1500, it is impossible to tell whether the number is accurate only to hundreds, or to tens, or to ones; the best guess in this case is that there are two significant figures, the one and the five, and the number is accurate to 1500 ± 100. If we write the number as 1.500 * 10³, however, the zeros to the right are important, and we have four significant figures; the value is accurate to 1500 ±1.

This format requires that we use exponential notation to keep track of the actual order of magnitude of the number. We move the decimal place to the left (if the exponent is negative) or right (if the exponent is positive) of its position in scientific notation according to the exponent on the "times 10" part of the notation.

Check your understanding of the way scientific notation is used for a particular example. Consider the number below, and when you are ready, guess the number of significant figures in it and its order of magnitude.

1.406 * 108 km

The Small Angle Formula

The small angle formula is based on a trigonometric proof that sin x ~ x for very small angles, where x is expressed in radians. For those of you who need some introduction or review of trigonometry (don't panic if you haven't seen this before, because it isn't that hard), here's the scoop on sines, cosines, and tangents.

Consider the right-angle triangle in the diagram. D is the hypotenuse, and D_y and D_x are the sides. The angle between D_y and D_x is a right angle, and the angle α is the angle we will use for various trig relationships (we could use the angle in the other corner and invert the relationships).

The trigonometric relationships give the ratios of the sides to the hypotenuse and to each other. Notice what the angles are when the trig relationships are maximum or minimum in value. This will help you keep them straight and do quick and dirty calculations when you don't have a calculator around.

sin α	Dy/D	0 when α is zero, 1 when α is 90 degrees.
cos α	Dx/D	1 when α is zero, 0 when α is 90 degrees.
tan α	Dy/Dx	1 when α is 45 degrees, 0 when α is 0, and infinity when α is 90 degrees.

Now, we can express α in degrees (360 to the whole circle, 90 to a quarter circle, etc.) or in radians. A radian is equal to the angle given when the radius r is laid around the circumference of the circle. Since C = 2*π*r, a radian is equal to 360/2*π, or about 57 degrees. An angle of α degrees is equal to α/(360/2*π) radians. If α is in minutes, the angle in radians is α/(360*60/2*π); if α is in seconds, the angle in radians is α/(360*60*60/2*π) = α/(206265)

Consider, now, the situation where a is the angle of separation, d is the distance to the object. To get a right triangle, we have to consider the triangle with angle a/2 and sides d and D/2. The trig relationship is

tan (a/2) = (D/2)/d

For a very small angle x, tan (x) ~ x if x is expressed in radians. Assuming that a/2 is small enough to be in seconds, then (a/2) = (a/2) /(206265)

(a/2)/(206265) = D/(2*d)

We cancel the factor 1/2 on each side and wind up with the small angle formula: a/206265 = D/d or D = a*d/(206265).

Units in Astronomy

The standard international system of units is based on meters, kilograms, and seconds. For most astronomical purposes, measurement in meters is too cumbersome. The distance from the earth to the sun in meters is 1.496 * 10¹¹ m. Even expressing this in kilometers doesn't help much (1.496 * 10⁸ km). Nor is it easy to see the relationships among planetary distances from the sun when all are expressed in these units. But if we take the distance from the earth to the sun as 1 of some unit (call it, say, an astronomical unit and give it the abbreviation AU), then we can look at solar system distances and make easy comparisons. Mercury is .37 AU or about 1/3 the distance between the earth and the sun; Jupiter is 5.2 or five times as far from the sun as earth.

Another unit in common astronomical use is the light year, or the distance light travels in one year. This is about 9.46*10¹²km, or 6 trillion miles. Use of the light year keeps us in mind of the fact that when we look at something very far away, we see it the way it was when the light left the object. The star Vega is about 37 light years away, so when we look at it tonight, we see it the way it was 37 years in the past. The further away the object is, the further back in time we are looking. The light year is useful for distances between objects within the galaxy.

Finally, we also use parsecs, or the distance from earth at which the diameter of the earth's orbit around the sun would subtend or make an angle of 1 second of arc. This distance is about 3.26 light years, so the parsec is used where light years aren't big enough, and often appears in measurement of distances between different galaxies.

Discussion Questions

• How do Kaufman and Freedman's explanations of scientific method, theory, and hypothesis compare with those in other science texts that you have read?
• Why are models so important to astronomy?
• Why are units important? Who determines what units can be used?
• What is our single source of information about other objects in the universe?
• What kinds of objects exist in the solar system? In the galaxy? In the universe at large?

Optional Readings

Each week, I'll try to recommend some of the better web sites around for particular topics in astronomy. I will not test you on the content of these sites, so don't feel compelled to visit them! Some you may find useful in offering alternative explanations for concepts you have difficulty understanding; you'll have to pick and choose according to the amount of time you have available.

Michael Fowler has an excellent site at the University of Virginia on the history of astronomy. You can read his summary of Aristotle's contributions to astronomy or explore the rest of his site -- he has a number of lectures published on the web for his course on Einstein and Galileo.

One of the best online astronomy texts is Nick Strobel's introduction to astronomy, written for his Bakersfield, California, junior college course. [Click on Jump ot Chapters listing to view the site contents.] I will be referring to this text from time to time, as it has a lot of good graphics, but be forewarned: graphics take time to load, so don't check out this site when you are in a hurry. For this week, you may want to take a look at the introductory material and scale model pictures of the solar system to get an intuitive sense of the relative sizes of the planets and their distances from the sun.

The Astronomiae Historia site has lots of links on the history of astronomy.

---

© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.