Course Icon

Astronomy

Lab: Using Parallax

SO Icon

Astronomy Lab Instructions

Stellar Motions and Distances

Goal: To Measure Parallax

Materials and tools

Procedure

  1. Tape paper together to make a strip at least 1 meter long. Draw a straight line down the 1m length the paper and mark it at 10cm intervals.

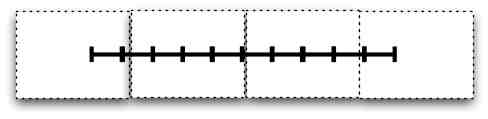
    ParallaxTape

  2. Position the paper on a wall or window such that you can stand at least 8 feet away.
  3. Take your position between 8 and 12 feet from your meter grid. Measure your distance D to grid in meters.
  4. Hold your thumb up about 20 cm (8 inches, the width of a sheet of paper) from your eyes, and align it between the grid marks. Record the distance r1 to your thumb in meters.
  5. Close one eye and look at your thumb. Record its apparent position x1 against the background grid and which eye you are using.
  6. Close that eye and open the other. Record your thumb's new apparent position x2 against the background grid.
  7. Repeat the two measurements with your thumb at arm's length (X3, X4). Record the distance r2 to your thumb in meters.
  8. Measure the separation E between the center of your eyes (or use the "normal" value 2.5in = 6.3cm).

Data Analysis

  1. Calculate the separation of the two measurements at the shorter distance S1 =|x2 - x1|.
  2. Calculate the separation of the two measurements at the greater distance S2 = |X2 - X1|.
  3. There are 360° in a circle = 2πr. If we set r = 1, we can calculate the ratio 360/2π = 57.3 and use this to convert linear distance to circumference degrees, or angular measurements.Convert your separation measurements to angular measurements in degrees using the relationship θ1 = S1 * 57.3°/(D - r1). Make sure that S1, r1, and D use the same units!
  4. Repeat your calculation for θ2 = S2 * 57.3° /(D - r2).
  5. We now have two proportional triangles, related by a common angle θ:

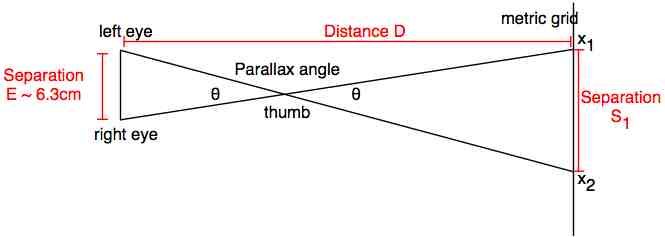
    Parallax3

    Using the separation E for your eyes, calculate the distance between your eyes and your thumb for the short position using r1 = 57.3°E / θ

  6. Repeat the above calculation for the distance to your thumb in the far position, using r2.
  7. Compare your computations for the distances to your thumb with the distances you measured. Are you calculations reasonable?
  8. The star ε Eridani has a parallax angle θ of 310.94 milliarcseconds (310.94 * 10-3arcsec). Can you determine the distance to this star using the Earth's baseline distance E = 2 * Earth's distance to the sun = 2 * 150 * 106km?

Data Table and Calculations

Trial Distance D observation position to grid Distance r to Thumb Separation S Angular measure
θ = S * 57.3°)/(D - r)
Far Separation with Thumb at close distance (20-25cm)
Far Separation Thumb at far distance (60-80cm)
Eye separation (20-25cm)
Eye Separation Thumb at far distance (60-80cm)

Report

Write a report of all your observations and post it to the lab assignment link at the Moodle.

  1. A description of the equipment and procedures you used in sufficient detail for someone else to repeat your experiment.
  2. All of your data, in tabular form if possible.
  3. All of your computations and conclusions for the data analysis section.
  4. Any other observations you think interesting or important.

© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.