
Natural Science - Year I
Unit 15: Forces and Equilibrium

Science Web Assignment for Unit 15
| This Unit's | Homework Page | History Lecture | Science Lecture | Lab | Parents' Notes |
Science Lecture for Unit 15:
Forces and Equilibrium
For Class
- Topic area: Applied mechanics
- Terms and concepts to know: Static equilibrium, center of mass
- See historical period(s): Roman Engineering
Outline/Summary
Equilibrium: Net Force of Zero
Forces and fixed objects. Forces acting on fixed objects, that is, an object held in place, can make parts of the object move. A force can compress, stretch, bend, or twist matter. The ability of materials to resist this kind of pressure or stretching determines whether the material will be useful for a particular situation. For example, concrete doesn't have very good tensile strength or shear resistance: if you pull on it, or twist it, it will break. But it has very high compression strength, so concrete is a good material where we want something to resist pressure, as in the pillars of a building.
We've already learned a bit about force in looking at machines. Forces cause objects to accelerate — to change their speed or direction. So any time we have a net force operating, we have acceleration, and we have motion.
It is important to note that force always causes a change in the existing motion (or lack thereof). If an unopposed force is acting, the object will speed up or slow down, or change direction. But no force is necessary to keep an object moving once it has started moving. If we have an object that is moving with a constant speed in a straight line, there is no net outside force acting on the object. If it changes speed or direction, some outside force is acting on it.
Obviously, if we want to build a road or bridge or building, we want the net forces on the construction to be zero. Otherwise some part or all of the building will move, and the building will come apart and fall down. In order to get all the forces operating on an object to sum to zero, we need to identify them and balance them.
Center of Mass
To understand how forces can cause different kinds of motion in an object, we have to understand the concept of the center of mass. We touched briefly on this in the last unit, but here we consider the concept more fully. Consider a bar of iron, balanced on a fulcrum. The gravitational pull on masses on one side of the fulcrum are balanced by gravity's pull on masses on the other side of the fulcrum. When the masses are not the same, the rod will tip to one side.

The center of mass is the point at which the object can balance on a fulcrum. Depending on the shape of the object and the distribution of matter in the object, the center of mass point can be to one side, or even outside the body itself! For example, the center of mass of a doughnut is in the hole, and there is no way to balance the doughnut on a single point if we want to lay it flat. Instead, we have to use two or more different forces acting on actual points of donut matter and in opposition with each other to balance the donut.
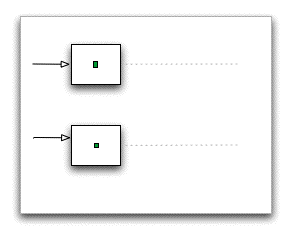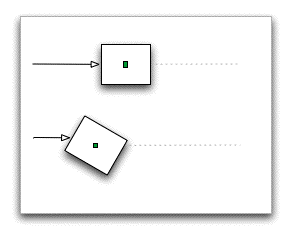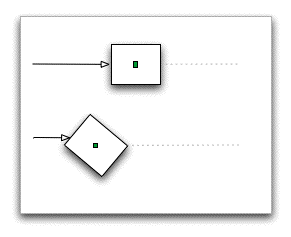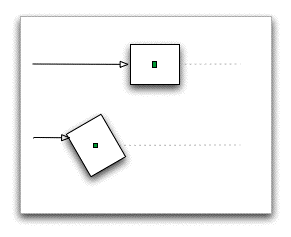
A short review: Forces can cause two kinds of motion in an object. If we push in a direction where the line of force passes through the center of mass, the object will move from one place to another. This is called translational motion. In the diagram of at the left, the small green box marks the center of mass in the rectangular object. The top situation shows a force pushing along a line through this point. If we want to prevent this motion, we need to exert a net equal and opposite force through the center of mass.
If we push in a direction where the line of force is off-center, the object will rotate around its center of mass, with rotational motion. The bottom situation shows a force acting along a line that passes above the line through the center of mass, so the object rotates. The magnitude of this force or torque is product of the magnitude of the force and the minimal distance from the line of force to the center of mass. If we want to prevent the rotation, we have to exert a net torque equal and opposite to the original torque, but this force doesn't have to act along the original line of force supplying the torque; it merely needs to oppose the direction of rotation caused by the torque.
Forces in Equilibrium
When we build a structure like a bridge or house, we try to balance all the forces on each part of the building. We have to make sure that all the translational forces sum to zero so some part of the building doesn't move from side to side or up and down. We have to make sure that off-center forces don't cause some part of the building to twist or rotate around another point. In the diagram at the right, we can see how the tension on a wire supports a rod (like a flagpole) so that the rod's weight doesn't pull it down or out of the wall. When architects or engineers design buildings, they have to make certain that all forces, both rotational and translational, are balanced.

Forces on the Material
Forces act on the individual atoms at the surface where, and even if the beam doesn't move, the atoms inside it may move slightly in response to these forces. Forces that pull the atoms apart (like the force on the wire, above) are called tension forces. Forces that push atoms in a single object together are called compressive forces. Forces that push atoms across one another are shear forces. A good example of shear force occurs when an earthquake pushes the base of a bridge support in one direction and the place where the bridge is attached to the river banks in a different direction.

Engineers must chose the correct materials in making structures so that the compression and tension forces don't shatter the materials. Concrete is a great material where resistance to compression is required, such as in pillars or basement floors, but concrete does not resist shear forces well. When it is used in pillars, the pillars are often reinforced with steel cabling, which provides resistance to tension and shear.
Study/Discussion Questions:
- What kinds of forces cause motion of a structure?
- What kinds of forces operate on the matter of a structure?
Further Study/On Your Own
- No external links at this time.
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.