
Astronomy
The Nature of Stars

Weblecture
The Nature of Stars
Stellar Spectra
Introduction
Teaching man his relatively small sphere in the creation, it also encourages him by its lessons of the unity of Nature and shows him that his power of comprehension allies him with the great intelligence over-reaching all.
— Annie Jump Cannon
How we Know what we know about Stars?
Given that the only observational information we have on stars is the light we receive, you might think there isn't much we can learn about them. But by comparing positions, brightness, and spectra over time, and comparing these with observations of our own star, the Sun, we can actually create accurate models that explain and predict stellar characteristics and behavior.
Star Names and Locations
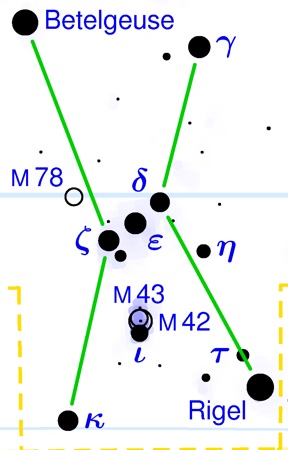
Most of our modern star names come from either Greek or Arabic names that were included in the classical Arabic manuscripts that became part of the medieval European university tradition. While these names are useful in identifying the more popular stars, they do not in and of themselves tell us anything about the nature of the stars they name. Around 129 BC, Hipparchus compiled a star catalogue, using the Greek letters to designate stars of 1st through 6th magnitude, with the faintest starts 100 times less bright than the brightest stars. This naming convention is still used for visible stars: α Centauri is the brightest star in the constellation Centaurus; ε Eridani is the 5th brightest star in Eridanus. In this diagram of Orion, Betelgeuse is α Orionis, and Rigel is β Orionis; Bellatrix is γ Orionis, Mintaka is δ Orionis, and the stars are brighter to fainter in that order.
[Hipparchus' original catalog was lost in antiquity, although used to Ptolemy in creating the catalogue in the Almagest. Recents studies of the Farnese Atlas (now in the museum in Naples) have convinced some scholars that the globe was made using Hipparchus' catalogue.]
Parallax
Parallax is the change in position of near objects against the background distant objects as an observer moves a short distance. In the first picture below, the Eiffel Tower, the church steeple, and the nearby bridge lamppost are aligned. In the second, the lamp appears far to the right, the steeple has shifted barely to the right, because the observer moved 15 paces to the left. (The change in magnification was required to frame the picture).


By using observations in January and June (or any other positions 182 days apart), astronomers can maximize their parallax baseline to 2 AU, the diameter of the earth's orbit. The convention, however, is to use the radius of the orbit, or 1 AU as the baseline in reporting measurements.
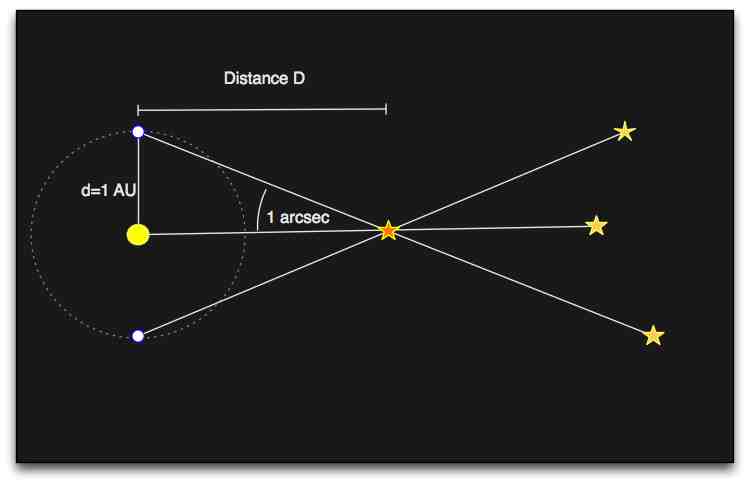
We can use the small angle formula, with d = baseline, D = distance to the star, and angle in arcseconds:
Brightness, Magnitude, and Luminosity
In the 19th century, astronomers standardized the magnitude scale, formally mapping magnitudes one through six to a scale that recognized Hipparchus' estimate that a 1st magnitude star was 100 times brighter than a 6th magnitude star. A change of five magnitudes equals a 100 times increase in brightness: Δ 5M = 100 brightness. This means that a change of one magnitude is equal to 5√100 = 2.51 times change in brightness, i.e, a first magnitude star is 2.51 times brighter than a second magnitude star. The scale has long since been extended to allow us to measure the sun (magnitude equals -26) and the faintest stars visible from ground-based telescopes (magnitude equals +22).
We can write the magnitude-brightness relationship mathematically as
Permutations on this formula are very powerful in calculating luminosities and distances.
Magnitudes are usually reported as observed in the visual range, but astronomers may take observations in the ultraviolet and blue ranges as well, since comparisons of these magnitudes can tell us something about the surface temperature of the star (see below).
Observed magnitudes, however, are affected by the distance of the star. Two stars of equal luminosity or brightness will appear to have different magnitudes if they are at different distances from the observer. In order to allow us to compare brightness and luminosity, as well as magnitudes directly, magnitudes are often reported as absolute magnitude. The absolute magnitude is the magnitude of star would have if it were observed at a distance of 10 parsecs. The absolute magnitude of the sun is +5. A star 100 times as bright as the sun would have an absolute magnitude of zero. A star 100 times fainter than the sun would have an absolute magnitude of +10.
The difference between the absolute magnitude and the apparent magnitude is given by a formula called the distance modulus, derived from the relationship between magnitude and brightness, given that the total luminosity of the stars not going to change when it is compared to itself.
| We start with the magnitude-brightness relationship: | |
| and the luminosity-brightness-distance relationship: | |
| We solve the latter to isolate brightness: | |
| then recognize that in the case of a star compared with itself, luminosity is not going to change: |
|
| We substitute in the distance for brightness: | |
| and recognize that an exponent in a logarithmic function becomes a multiplier |
|
| Substitute apparent magnitude (m = m2) and absolute magnitude (m1 = M) and the distance d1 = 10 pc We also separate out the factors of the log (using the rule log (a/b) = log a - log b) |
|
| Finally, we recognize that log 10 = 1 |
Luminosity is also a measure of the total energy output of the star, which closely resembles a black body. We've already seen how temperature can be related to the wavelength of greatest intensity
When we solve for T and express λmax in nm (10-9m), this equation becomes
Practice with the Concepts
Optional Readings
- The Origin of the Hertzprung-Russell Diagram page gives you a bit of background on the origin of this most useful of graphic representations
- Another set of notes on the first HR diagram published, with a picture of Karl Schwarzschild and Ejnar Hertzprung taken around 1909.
© 2005 - 2025 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.