Solubility

Outline

• Solubility
• Practice with Concepts
• Discussion Questions
• Optional Website Reading

Solubility

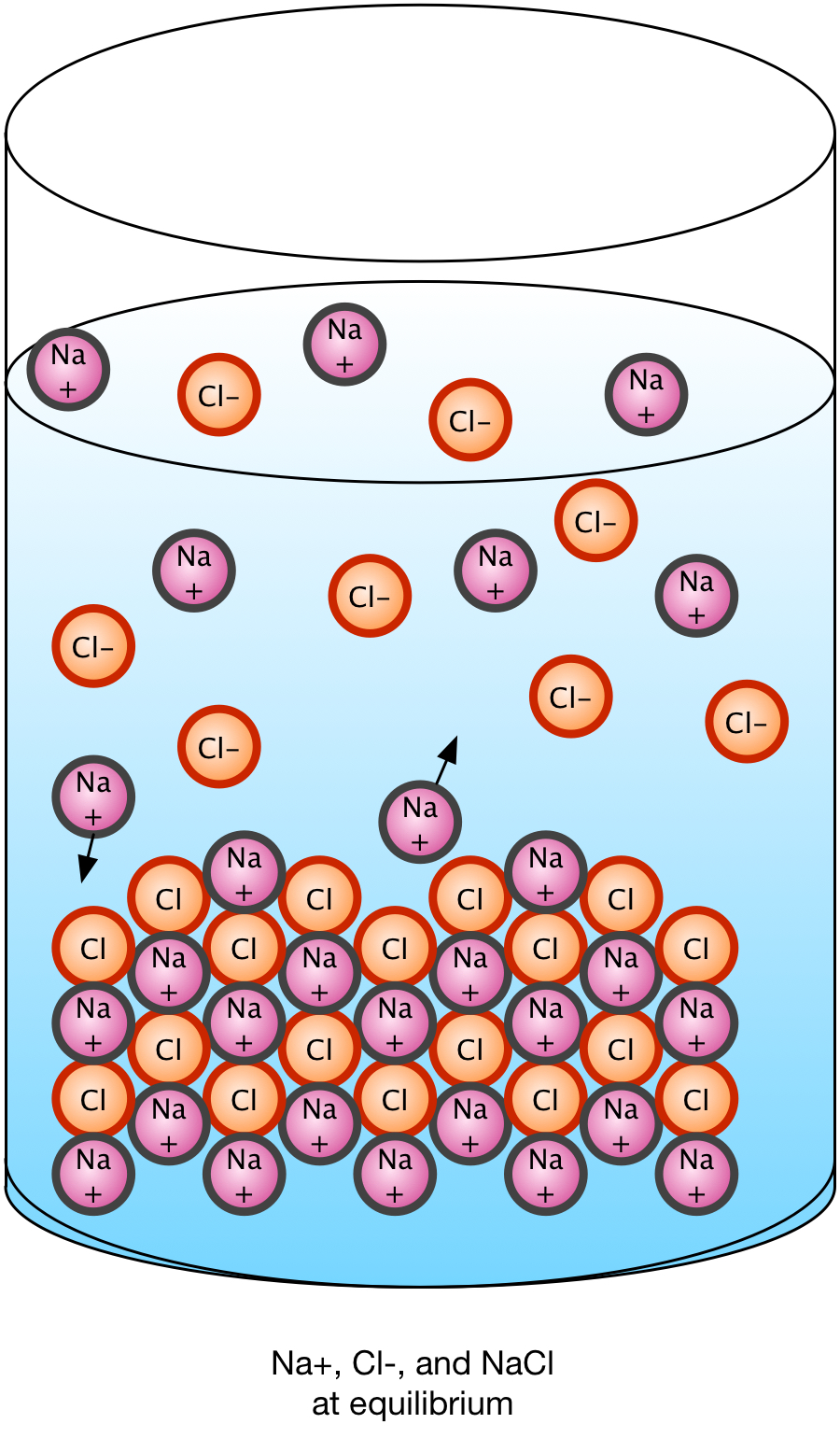
Solubility is a measure of how much an ionic solid dissociates in water to reach an equilibrium state between the water, the ions, and the solid form. Some solids, like sodium chloride, dissociate completely; others dissociate to a lesser degree, retaining some solid. The solution is then considered saturated and unable to hold any more ions. If we add ions to a saturated solution which is not in contact with a solid, solid precipitate will form until the equilibrium balance between ions, water, and solid is re-established.

If an acid and base interact, the cation of the base and the anion of the acid are freed to interact, or not. When NaOH and HCl interact, the ions are Na+ and Cl-, which remain dissolved in aqueous solution, because Cl- is soluble in all concentrations, according to our earlier summary of reactions. The solubility of a salt is the amount present in a saturated solution, at the point where any additional cation or anion will cause the dissolved ions to precipitate. It is an amount (grams, moles) per unit volume (mL, liter).

We can, however, be somewhat more quantitative now that we have talked about reaction quotients Q and equilibrium constants K, and designate another "K" value for the concentrations of the cation and anion present at saturation. K_sp is the solubility product for the reaction of dissociation of an ionic solid in aqueous solution. If we have a reaction

A_aB_b → aA- + bB+

p>the equilibrium constant will be $$K_{\mathrm{sp}}=\frac{{[A-(\mathrm{aq})]}^a{[B+(\mathrm{aq})]}^b}{\mathrm{AB}(s)}={[A-]}^a{[B+]}^b$$

The smaller the K_sp value, the less the solid form of the compound dissolves. Remember that K_sp is in definition a ratio of concentrations, in this case, ions to solids.

If we let a simple ionic solid dissociate such that AB → A- + B+, the resulting concentrations of the dissociated ions [A-] and [B+] in a volume of water represent the change x in concentration from zero. K_sp = [A-][B=} = (x)(x) = x². So for simple ionic solids where the cation and anion exist in a 1:1 ratio, the K_sp of the solution is the square of the (equal) concentrations of the ions at equilibrium.

If we have a more complex ionic solid, then we need to take the coefficients into account. For example, if we have AB₂ → A- + 2 B+, then the value of K_sp = [A-][B+]² = (x)(2x)² = 4x². It is important to balance the dissociation equation before using the K_sp value to determine the equilibrium concentrations or solubility of a particular solute.

Now consider a saturated solution which also contains some of the solid. We have AB (s) ⇔ A-(aq) + B+(aq). Suppose that we add another compound, CB, which also dissociates because C is soluble in all situations. We have now increased the concentration of the common ion, B+. Le Chatelier's principle requires that the AB reaction run in reverse and form more precipitate AB(s). So adding a common ion will reduces the solubility of a saturated salt solution.

If the anion of the insoluble salt is the conjugate base of a weak acid, it will be a strong base which will react readily with water. Consider what happens if we dump a such a salt into a water solution (such as pouring it down the drain). We have the dissociation reaction as the first phase of a reaction system, supposedly going to equilibrium:

AB ↔ A- + B+

But now the anion reacts with water as well (a hydrolysis reaction):

A- + H₂O → HA + OH-

Because this second reaction reduces the concentration of A- in a solution which still contains AB, Le Chatelier's principle requires that more of the AB dissolve to replace the A- lost to the second reaction. The "insoluble" salt is suddenly much more soluble as its components react with available water molecules. We may wind up with a highly corrosive concentration of our "weak" base.

So it is important to consider the "secondary" reactions of the ions with their environment (in this case, with the water in the aqueous solution).

Obviously, there are several factors that affect the solubility of an ionic compound.

• The solubility of a salt depends on its cation-to-anion ration. Comparing K_sp values of two salts is useful only when the cation-to-anion ratios are the same. We can compare silver iodide (AgI) solubility to silver chloride (AgCl) solubility using only the K_sp values, because both cases have a 1:1 ratio of anion to cation. We can't compare lead iodide (PbI₂) to silver chloride (AgCl) because PbI₂ has a 1:2 ratio of cation to anion.
• As we saw above, the solubility of a salt is reduced if we add a common ion to a solution. A salt dissolution reaction is a solid reactant to ionic product dissociation reaction, so adding ions increases the concentration of the products, driving the dissociation reaction backwards to increase the reactant amount as the system tries to re-establish equilibrium by reducing the product ion amount.
• Any salt containing an anion that is the conjugate base of a weak acid will dissolve in water to a greater extent than you can predict from K_sp alone, as in the example above. The conjugate base anion will react with water (as an acid), reducing its concentration as the product of the dissolution reaction, and stimulating the system to replace the conjugate base through further dissolution.
• If we have an "insoluble" salt where the anion is the conjugate base of a weak acid, it will dissolve in a strong acid. The acid removes the anion, so the compound will keep dissolving as it tries to maintain its own equilibrium situation.

Discussion Question

• What are the environmental impacts associated with "unexpected" solubilities of insoluble solids?

Optional Readings

• There are some examples of solubility product calculations at the Purdue Chemistry website

---

© 2005 - 2024 This course is offered through Scholars Online, a non-profit organization supporting classical Christian education through online courses. Permission to copy course content (lessons and labs) for personal study is granted to students currently or formerly enrolled in the course through Scholars Online. Reproduction for any other purpose, without the express written consent of the author, is prohibited.